티스토리 뷰

▶차원 축소(Dimensionality Reduction)
차원 축소는 많은 feature로 구성된 다차원의 데이터 셋을 차원을 축소하여 새로운 차원의 데이터 셋을 생성하는 것을 말합니다.
다시말해서, 변수를 줄인다고 생각하면 됩니다.
이제 축소하는 방식에 대해 알아보겠습니다.
1) PCA
PCA(Principal Component Analysis)는 가장 대표적인 차원 축소 기법입니다.
여러 변수 간 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소하는 기법입니다.
간단하게 분산을 최대한 보전하는 데이터의 축을 찾아 차원을 축소하는데, 이것이 PCA의 주성분이 되는 방식입니다.

위 사진에서 데이터의 분산을 가장 잘 복원한 주성분은 무엇일까요?
당연히 c1이 되겠습니다.
그러므로 c1을 주성분으로 택하는 것입니다.
from sklearn.decomposition import PCA이제 PCA 객체를 만들어보겠습니다.
- n_component : 1보다 작은 값을 넣으면 알아서 분산을 기준으로 차원 축소. 1보다 큰 값을 넣으면 해당 값만큼으로 차원 축소
pca = PCA(n_components=2) # feature를 2개로 축소하겠다위에서 PCA는 분산을 최대한 보존한다고 했습니다.
그러면 이상치에 대해서도 보존하려고 할 것입니다.
그렇기 때문에 표준화를 해주겠습니다.
+) 정규화와 표준화의 차이
◎ 정규화(Normalization)
- 값의 범위(scale)을 0~1 사이의 값으로 바꿔주는 것
- 학습 전에 scaling 하는 것
- 머신러닝에서 scale이 큰 feature의 영향이 비대해지는 것을 방지
- 딥러닝에서 Local Minima에 빠질 위험 감소(학습 속도 향상)
- scikit-learn에서 MinMaxScaler 사용
◎ 표준화(Standardization)
- 값의 범위(scale)를 평균 0, 분산 1이 되도록 바꿔주는 것
- 학습 전에 scaling 하는 것
- 머신러닝에서 scale이 큰 feature의 영향이 비대해지는 것을 방지
- 딥러닝에서 Local Minima에 빠질 위험 감소(학습 속도 향상)
- 정규분포를 표준정규분포로 변환하는 것과 같음
- scikit-learn에서 StandardScaler
① n_composition 지정 : 1 이상 지정
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)':'petal width (cm)'])방금 표준화시킨 데이터로 PCA를 진행합니다.
pca_data = pca.fit_transform(data_scaled)PCA를 적용한 데이터셋을 한번 출력해 보겠습니다.
pca_data[:5] # 차원이 2개로 축소되었음을 확인 가능out:

차원 축소한 데이터셋을 시각화 해보겠습니다.
import matplotlib.pyplot as plt
from matplotlib import cm
import seaborn as sns
# 시각화 도구 포함
%matplotlib inlineplt.scatter(pca_data[:, 0], pca_data[:, 1], c=df['target'])out:

② n_component 자동 : 1 이하 지정
pca = PCA(n_components=0.99) # 1보다 작게 입력하면 분산에 의해 알아서 계산해서 자동으로 지정pca_data = pca.fit_transform(data_scaled)
pca_data[:5]out:
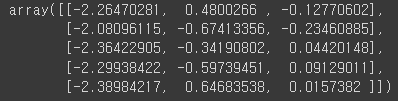
PCA가 적용된 데이터 셋을 시각화 해보겠습니다.
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection='3d')
sample_size = 50
ax.scatter(pca_data[:, 0], pca_data[:, 1], pca_data[:, 2], alpha=0.6, c=df['target'])
plt.savefig('./tmp.svg')
plt.title("ax.plot")
plt.show()out:
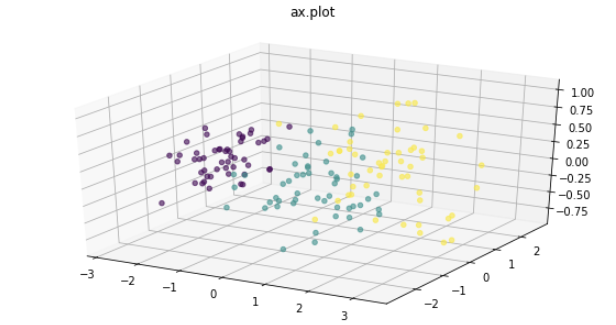
2) LDA
LDA는 선형 판별 분석법으로 불리며 PCA와 매우 유사합니다.
LDA는 PCA와 유사하게 입력 데이터 셋을 저차원 공간에 투영해 차원을 축소하는 기법이지만,
중요한 차이는 LDA는 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소합니다.
따라서 클래스(class) 분리를 최대화하는 축을 찾기 위해 클래스 간 분산과 내부 분산의 비율을 최대화 하는 방식을 이용합니다.
LDA가 진행되는 순서는 다음과 같습니다.
- 클래스 내부와 클래스 간 분산 행렬을 계산
- 클래스 내부 분산 행렬의 역치 행렬과 클래스 간 분산 행렬의 곱을 분해하여 고유벡터와 고유값을 계산
- 고유값이 가장 큰 순으로 k개 추출
- 추출된 고유벡터를 이용해 입력 데이터를 선형 변환
from sklearn.discriminant_analysis import LinearDiscriminantAnalysislda = LinearDiscriminatAnalysis(n_components=2) # 2차원으로 축소
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)':'petal width (cm)'])
lda_data = lda.fit_transform(data_scaled, df['target'])차원 축소한 데이터들을 시각화 해보겠습니다.
plt.scatter((lda_data[:, 0], lda_data[:, 1], c=df['target'])out:


여기까지 차원 축소에 대해 공부해 보았습니다 :)
'빅데이터 인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝] ⑫ 군집화(Clustering) in 비지도학습 (0) | 2022.08.24 |
|---|---|
| [머신러닝] ⑪ 하이퍼 파라미터 튜닝을 쉽게 (0) | 2022.08.23 |
| [머신러닝] ⑩ 교차 검증(Cross Validation) (0) | 2022.08.23 |
| [머신러닝] ⑩ random_state에 대해서 (0) | 2022.08.22 |
| [머신러닝] ⑨ 앙상블(Ensemble) 모델 (0) | 2022.08.21 |
- Total
- Today
- Yesterday
- 리액트 훅
- 자바스크립트
- 데이터분석
- 스타일 컴포넌트 styled-components
- styled-components
- Python
- 프론트엔드 공부
- 리액트
- 인프런
- 딥러닝
- 머신러닝
- react
- frontend
- next.js
- testing
- 프로젝트 회고
- rtl
- react-query
- HTML
- TypeScript
- 타입스크립트
- 자바
- 디프만
- JSP
- 파이썬
- 프론트엔드 기초
- 프론트엔드
- CSS
- 자바스크립트 기초
- jest
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
