티스토리 뷰

▶CNN(Convolutional Neural Network) A to Z
CNN이 등장하게 된 배경부터 구조까지 알아보려고 합니다 :)
1. CNN 왜 등장?
이전에 MLP글에서 ANN의 한계점(XOR 문제 해결 못함)을 보완하고자 MLP가 등장했다고 했었는데요.
결론부터 말하자면, ANN도 MLP의 한계점을 극복하고자 등장했습니다.
ANN 및 MLP의 한계점
- 이미지 input을 flatten을 함으로써 이미지 자체를 구성하고 있는 공간적인 정보를 충분히 활용 X
- 학습하는 파라미터가 굉장히 많음
- 각 pixel마다 들어있는 데이터(모든 픽셀에 대해서)를 바탕으로 해서 분류를 하기 때문
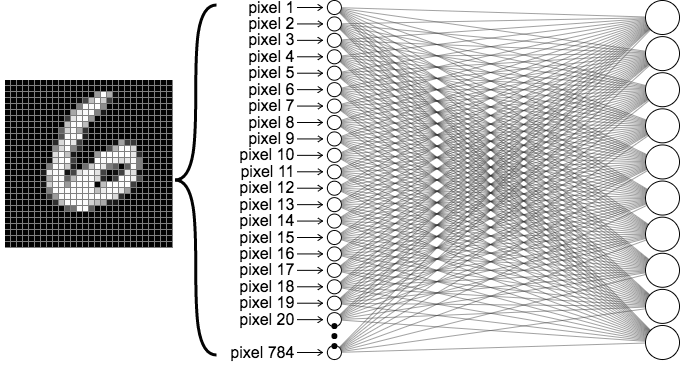
ANN은 이미지의 공간적인 정보를 활용하기 위해, 더욱 효과적으로 학습(특징 추출)을 하기 위해서 등장!
2. Convolution(합성곱)
- 두 function을 합성함으로써 새로운 function을 얻게 됨

위 식은 연속함수 f, g를 convolution 하는 식입니다.
먼저, 합성곱을 위해서는 두 함수 중 하나를 반전(reverse)시켜야 합니다.
위의 식을 보면 연속함수 g의 변수 타우 앞쪽에 마이너스가 붙어있는 것을 확인할 수 있습니다.
→ 함수 g를 반전(reverse)
다음으로, 반전시킨 함수를 전이(shift) 시켜야 합니다.
마찬가지로 위 식에서 함수 g를 t만큼 이동시킨 것을 확인할 수 있습니다.
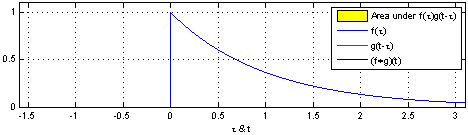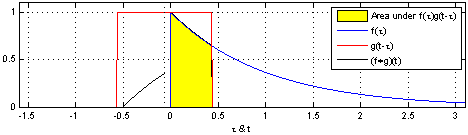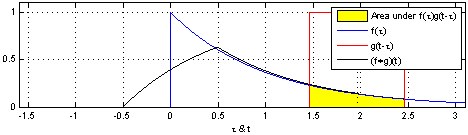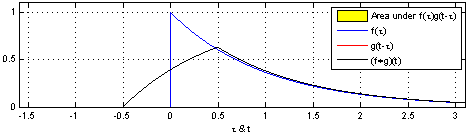
마지막으로, 이동시킨 함수 g를 함수 f와 곱한 결과를 하나씩 기록합니다.
이때 변수 타우를 변화시키며 결과를 쭉 기록하는 것을 convolution이라고 합니다.
어떨 때는 두 함수가 겹치게 되고, 또 어떨 때는 겹치는 게 없어서 합쳐도 0이 되기도 합니다.
2-1. 1D Convolution
- 벡터에 의해 Element-wise하게 muliplication
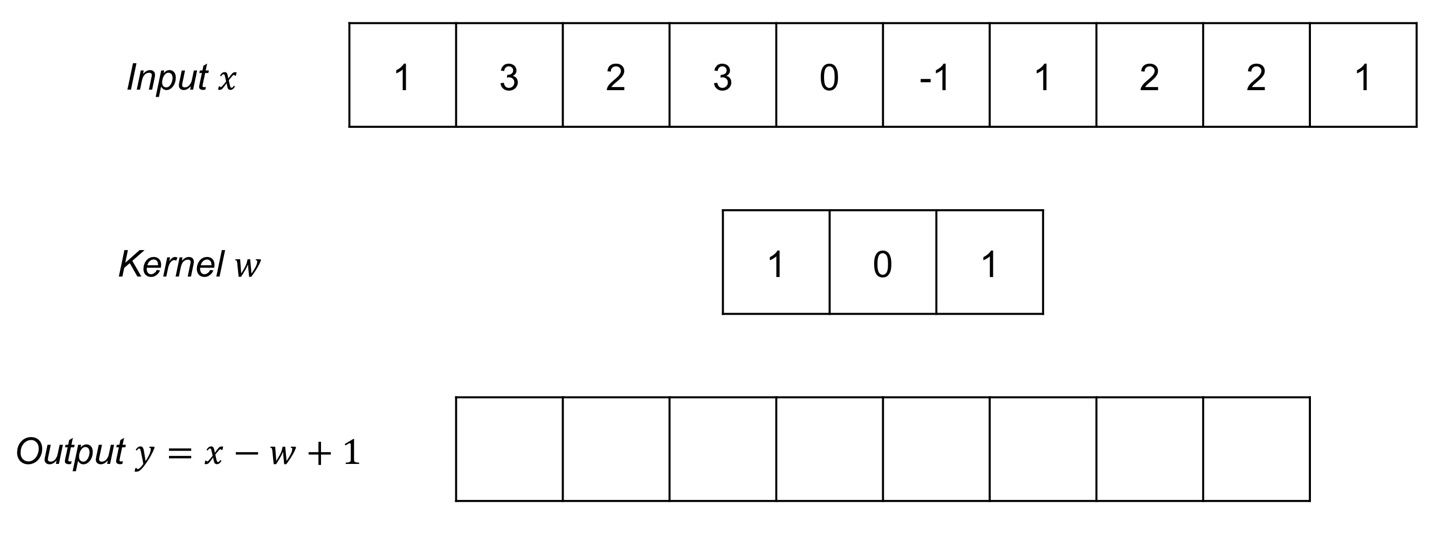
input function은 그대로 있고 kernel이 움직이면서 element-wise muliplication을 통해 새로운 output vector를 도출하게 됩니다.
계산하는 과정을 자세히 적어보면 아래와 같은데요.
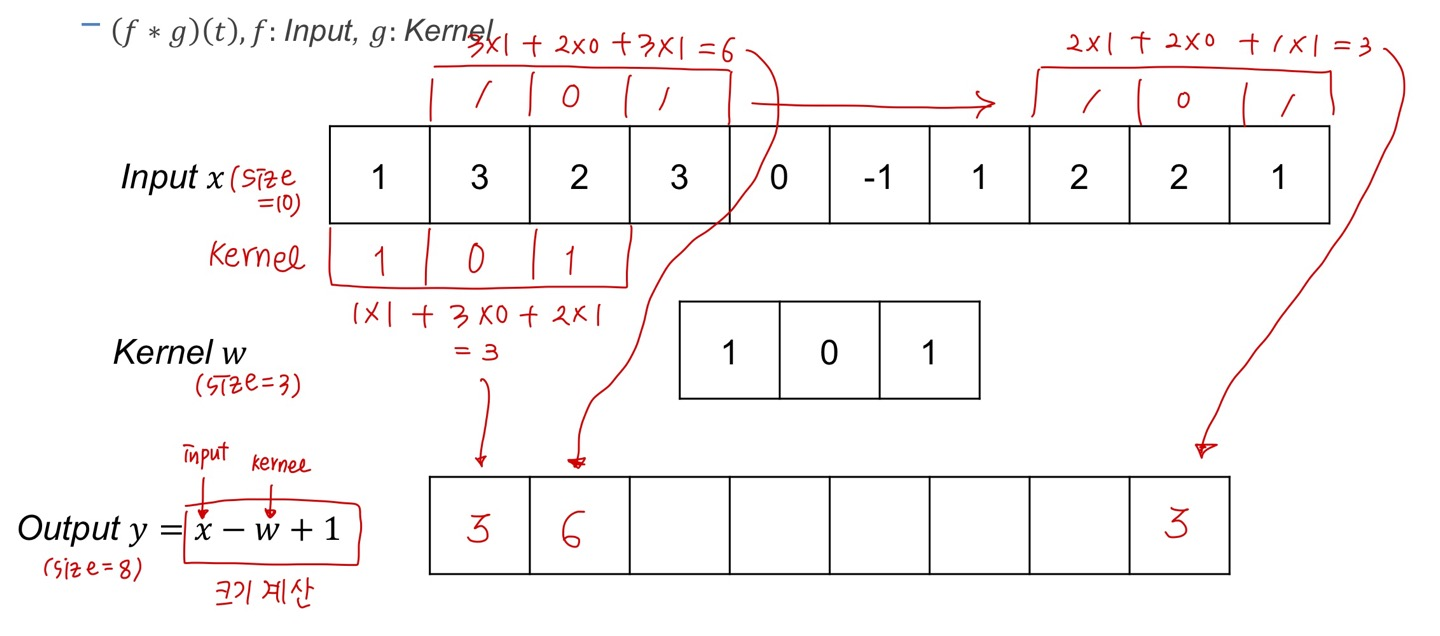
Convolution = multiplication & shift
이쯤에서 드는 의문...
그래서 Convolution은 왜 하는건데?
- 합성곱을 통해 데이터를 denoising 가능
- 합성곱을 통해 데이터에서 발견할 수 있는 edge들도 발견 가능
즉, 데이터로부터 어떤 filter(kernel)을 적용해서 새로운 정보를 얻어내기 위해 합성곱을 한다!
예를 들어 위 내용을 조금 살펴보겠습니다.
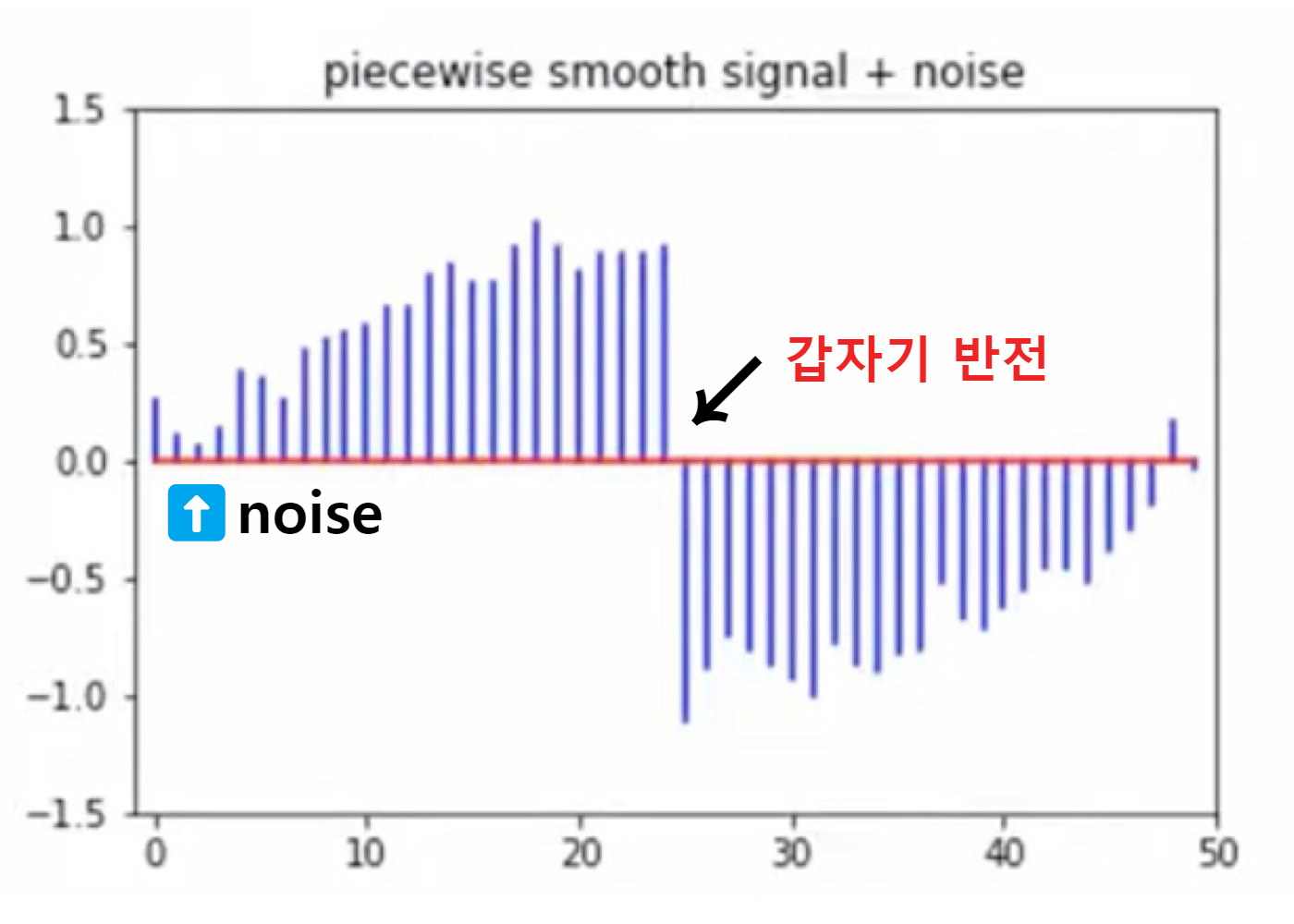
위와 같이 노이즈가 포함되어 있고 갑자기 25 정도에 반전이 일어나는 구성으로 이루어진 데이터가 있다고 해봅시다.
(지금 소개하는 kernel 값은 꼭 무조건 정답은 아닙니다!)
① Denoising | 노이즈를 없애서 데이터를 smooth하게
→ [0.25, 0.25, 0.25, 0.25] 커널과 데이터를 Convolution
데이터와 커널을 합성곱하게 되면 아래와 같은 새로운 데이터를 얻을 수 있게 됩니다.

② Edge Detection | 급격하게 변하는 부분 찾자, 나중에 이미지의 아웃라인을 찾을 때에도 도움
→ [-0.5, 0.5] 커널과 데이터를 Convolution
데이터와 커널을 합성곱하게 되면 아래와 같은 새로운 데이터를 얻을 수 있게 됩니다.

2-2. 2D Convolution
- 행렬에 의해 element-wise하게 multiplication
- 1D Convolution과 비슷하게 커널을 shift하면서 multiplication
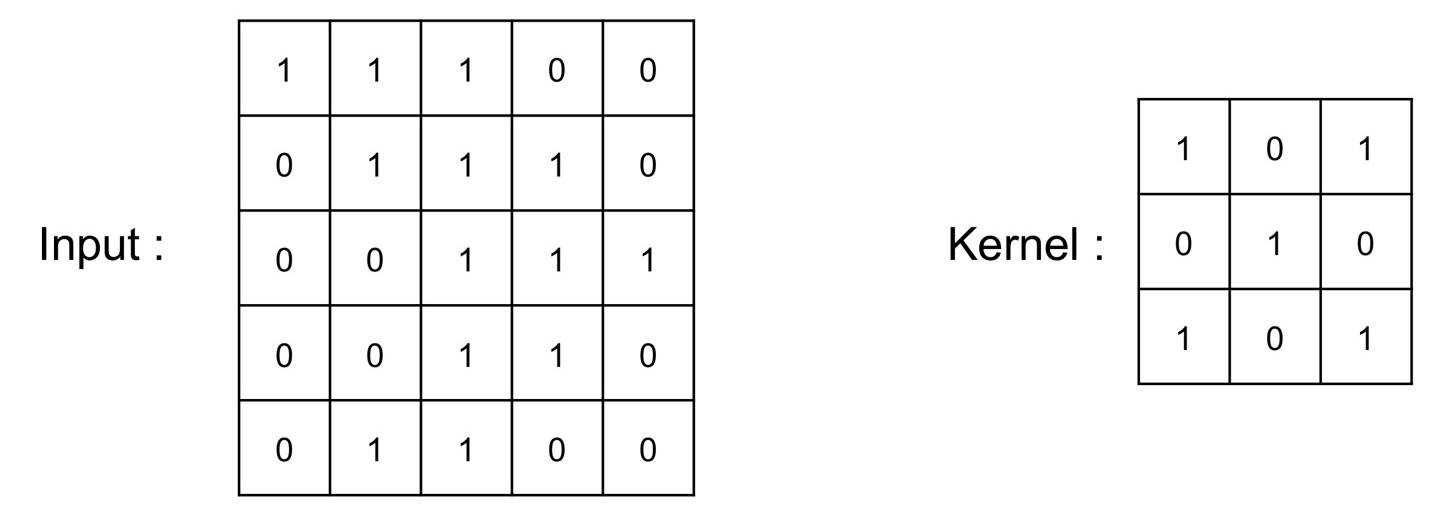
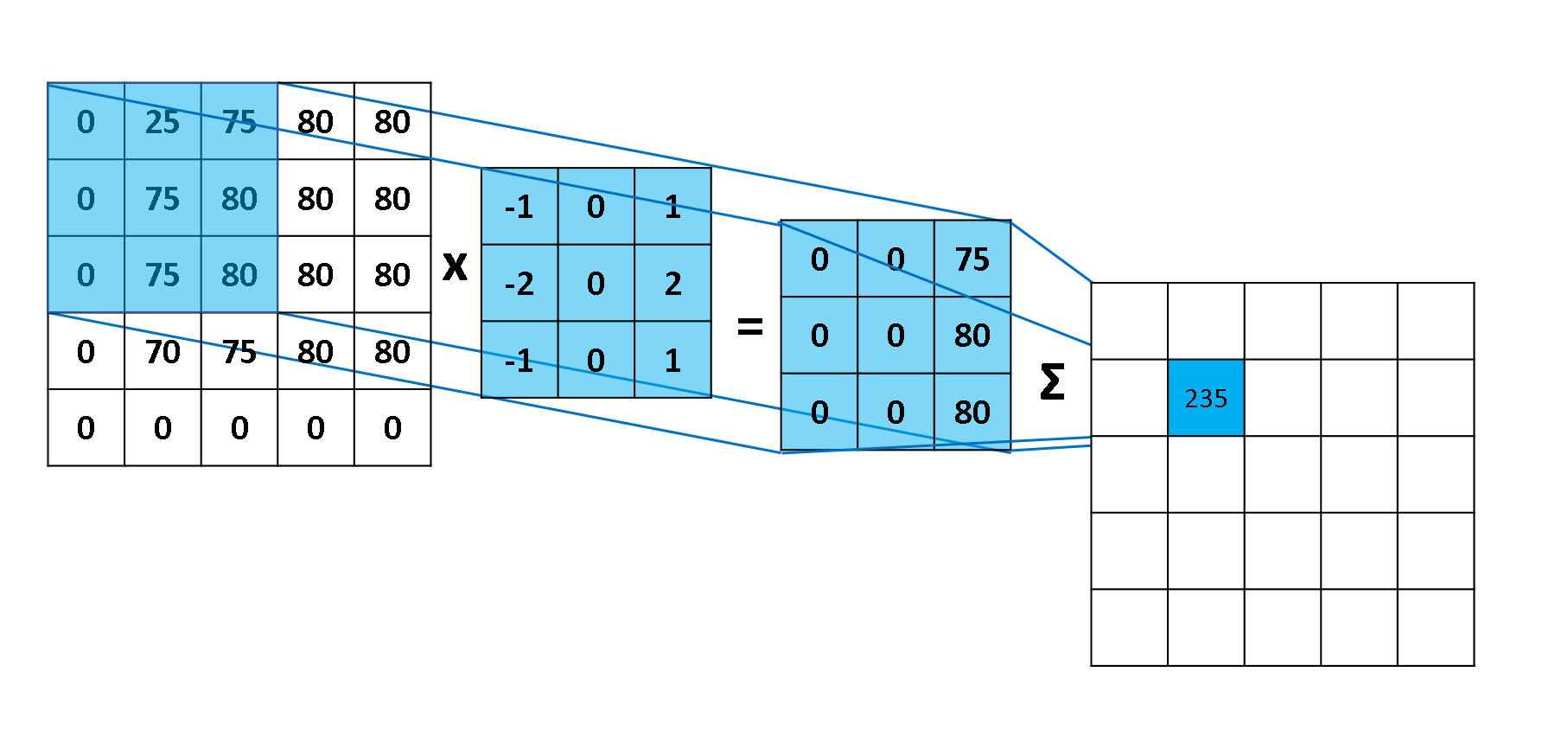
2D Convolution에서도 1D Convolution 때와 비슷하게 데이터를 smooth하게, 혹은 edge detection을 하거나 하는 필터를 적용하는 작업이 가능한데요.
좀 이미지에 이를 적용하여 설명하면, 이미지를 smoothing(Blurring) 하거나 아웃라인을 찾아내는 작업 등이 가능하다는 것입니다. 필터(kernel)를 통해서요!
- Image Smoothing (Blurring)
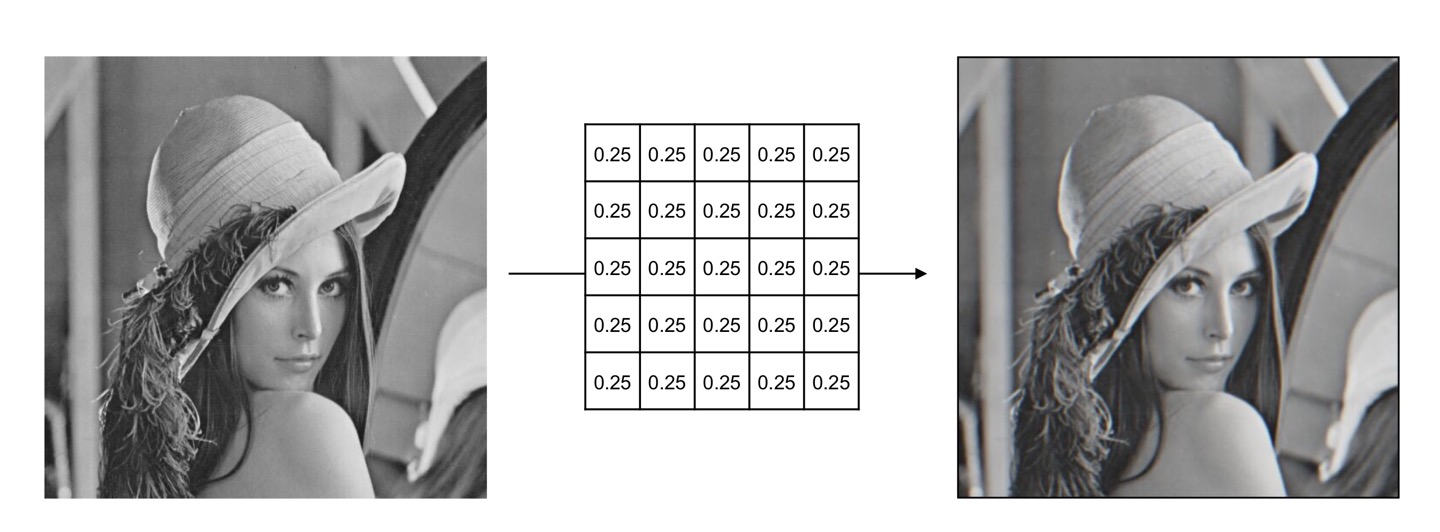
- Edge Dectection
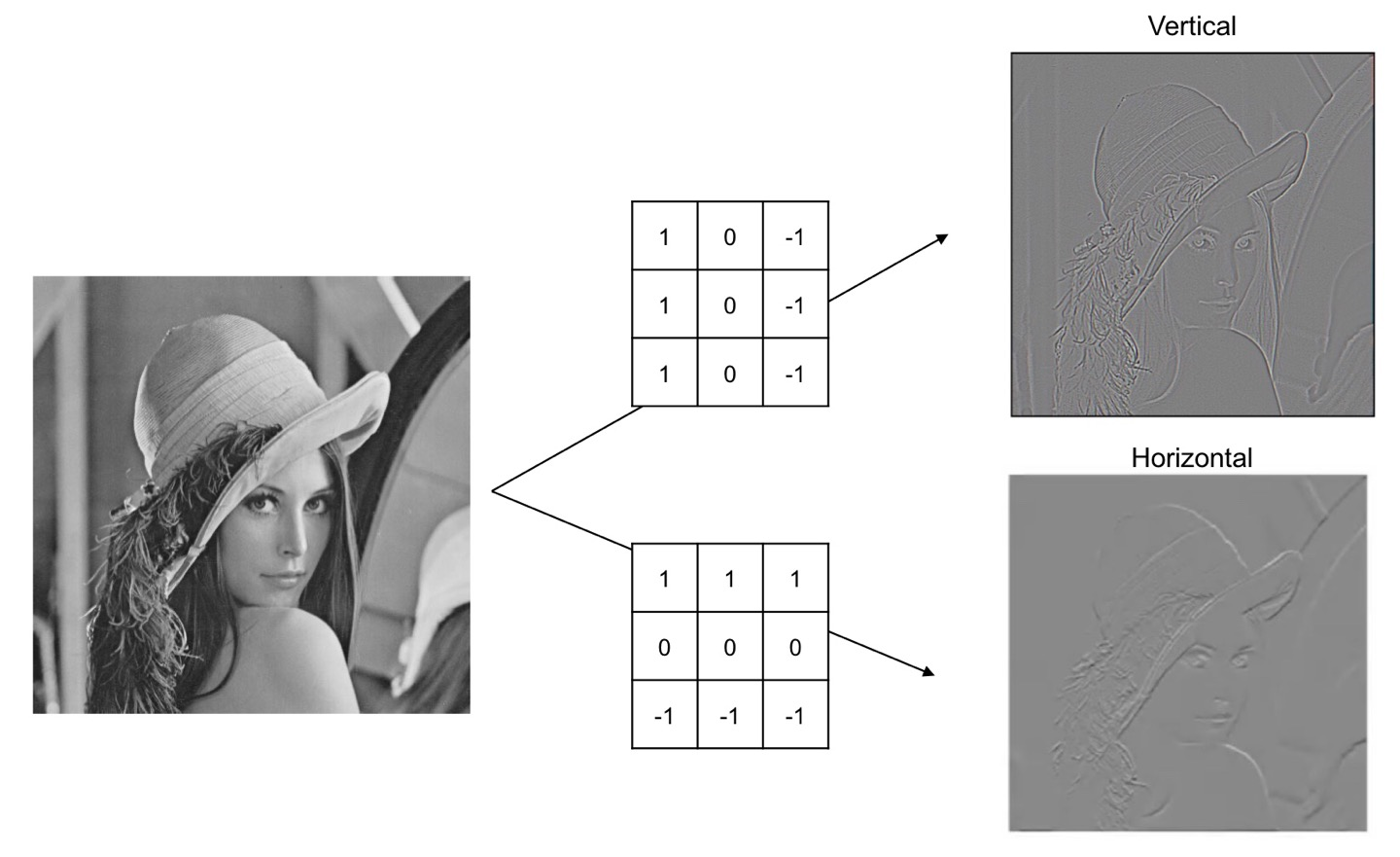
2-3. Kernels
우리가 앞서 계속 kernel..kernel...filter...했던 게 대체 뭔지 자세히 알아보겠습니다.
- 이미지 필터를 할 때 kernel은 중요한 역할을 수행
- 수동 방식으로 커널을 설계하지는 않음
- 왜냐하면 서로 다른 이미지들이 서로 다른 kernel을 요구하기 때문
- 딥러닝 프레임워크를 사용하여 데이터에서 feature 추출
3. Convolutional Neural Network
- region features를 학습하기 위한 접근법
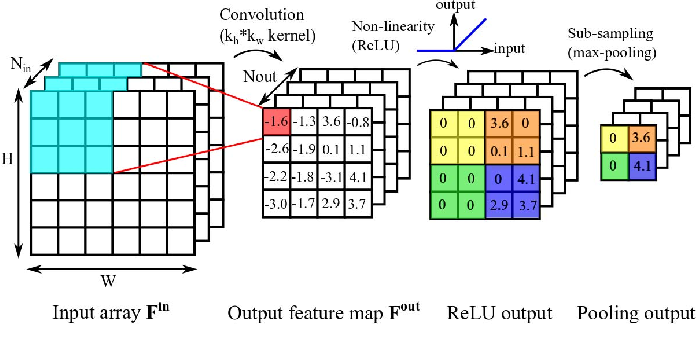
- Conv layers, Non-linearity, Pooling layers, and Fully Connected layer
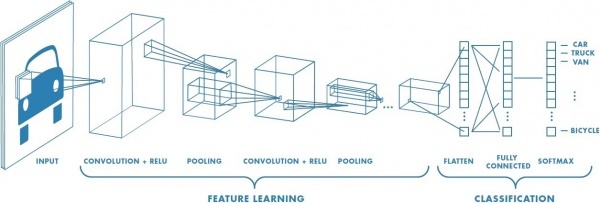
region features가 뭔데?
위 그림에서 맨 처음 input 이미지를 보게 되면, 사실 자동차 형태가 있으면서도 픽셀 단위로 보았을 때는 분류에 있어서 의미 없는 픽셀들도 존재합니다.
따라서 이미지의 중요한 부분의 특징을 추출하는 것이 분류 문제 해결에 중요 요소가 될 수 있겠습니다.
그러므로 FC layer만 있던 MLP와 달리
CNN에는 이미지의 중요한 특징을 추출하는 layer인 Convolution Layer와 Pooling Layer가 존재합니다.
특징 추출 : Convolution Layer, Pooling Layer
마지막으로 분류 : Fully Connected Layer
Multiple kernels
- 한 이미지에 대하여 여러 개의 커널을 적용하는 경우
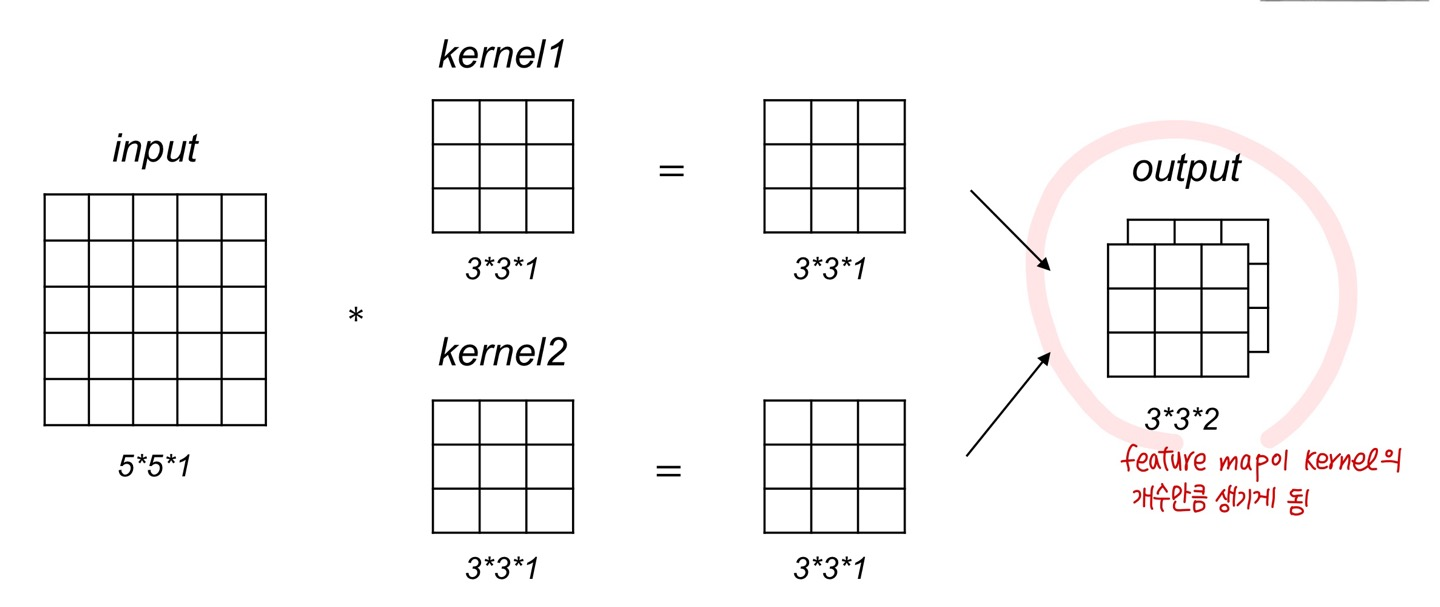
위에서 convolution을 살펴보았을 때처럼 커널을 shift하면서 multiplication 하면 됩니다.
위 경우에서는 kernel이 2개이므로 각 kernel에 대해서 convolution 해주게 되면 2개의 feature map이 나오게 됩니다.
Feature map
- 인풋 데이터 * 커널 연산의 결과
- Feature map의 수는 kernel 수와 같게 만들어 진다.
- 목적은 각각의 특징들을 패턴으로 읽어내는 것. 쉽게 말해서 특징을 잡아내는 map!
Multi-channel and Multi-kernel convolution
- 인풋 데이터의 채널도 여러 개, 커널도 여러 개라면
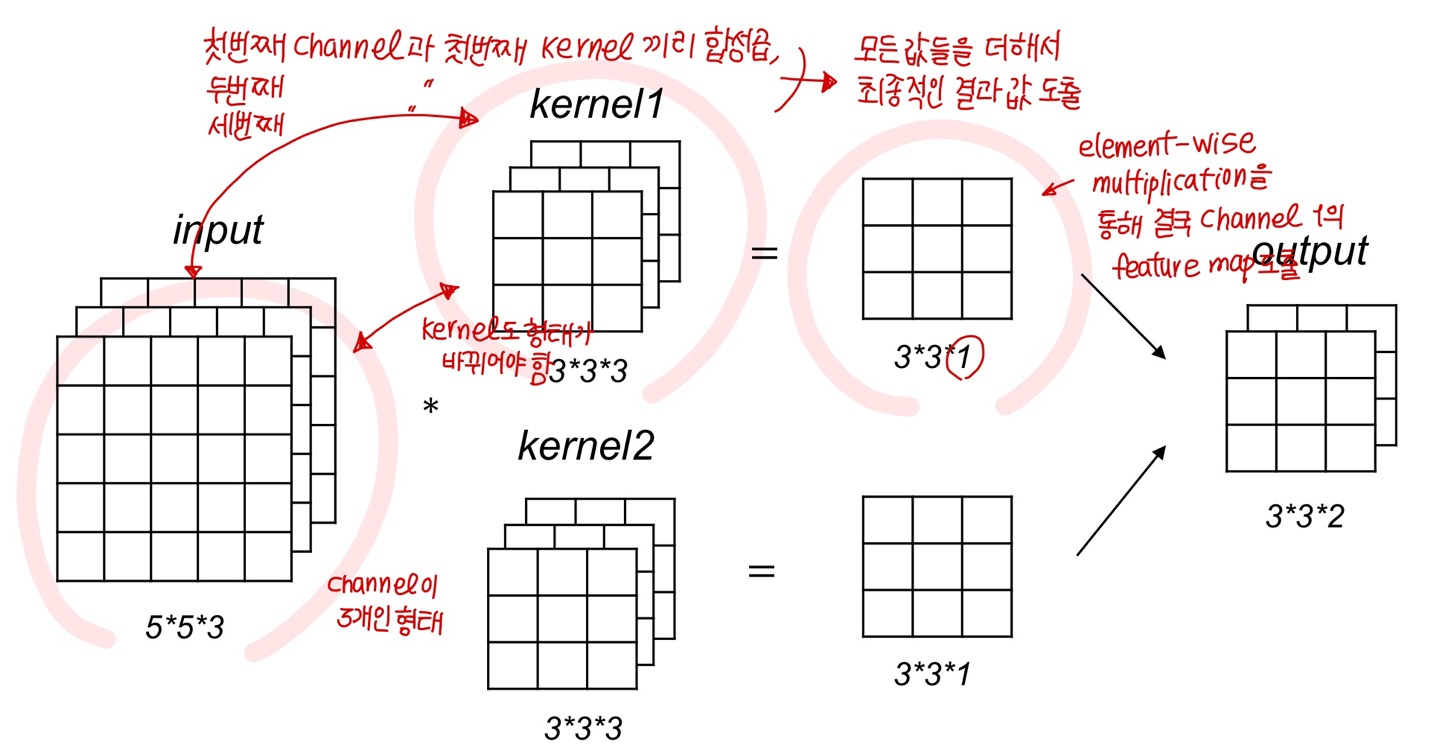
CNN의 특징
① Locality(Local Connectivity)
- CNN은 kernel을 이용해 feature map을 추출
- 이때 이런 kernel을 여러 개 적용하여 다양한 local 특징을 추출 가능
- Subsampling 과정을 거치면서 이미지의 크기를 줄이고 local feature들에 대한 kernel 연산을 반복적으로 적용하면
- 점차 global feature를 얻을 수 있게 된다

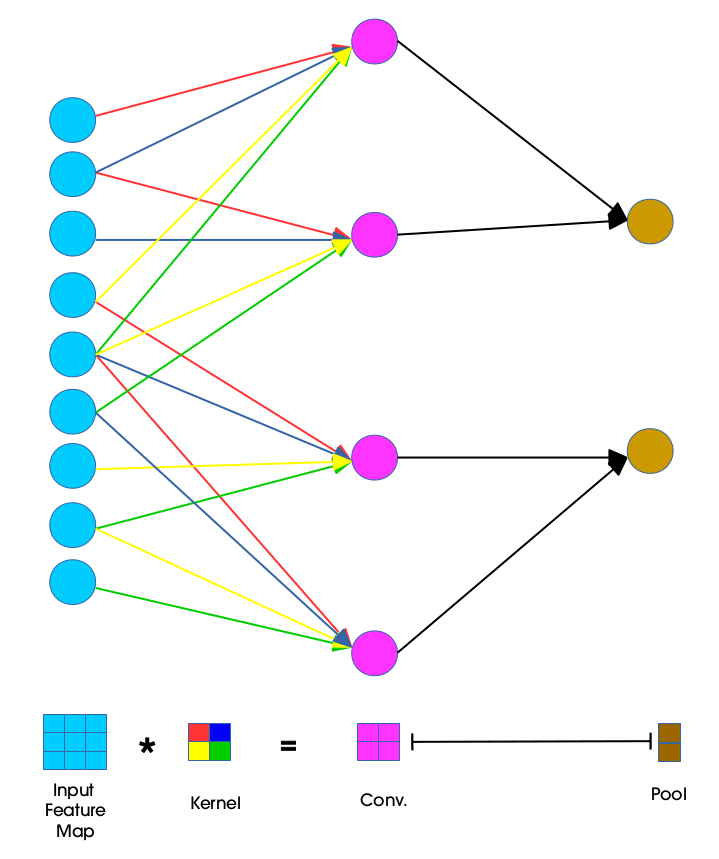
② Weight Sharing
- 모든 receptive field에 동일한 weight 사용
- kernel이 shift할 때 그 kernel에 대한 값이 변하지는 않았음
- 즉, 동일한 weight를 활용함으로써 학습을 좀 더 효율적으로 구축 가능
- MLP의 경우 하나의 출력값을 위해 각가 다른 가중치들을 사용 (Fully connected)
- 반면에 CNN은 하나의 출력값에 같은 가중치들을 사용 (이게 바로 weight sharing)
Padding and Stride
① Padding
- 이미지 데이터의 축소를 막기 위해 사용
- CNN 과정에서 여러 번 데이터와 kernel을 연산하다 보면 이미지 사이즈가 작아지게 되는 것을 막기 위해
- 이미지가 작아지면 안 되는 이유
- 더 깊에 학습시킬 데이터가 부족해지는 것
- 이는 Neural Network의 성능에 약영향
- padding의 종류
- 일반적으로 zero padding을 많이 활용

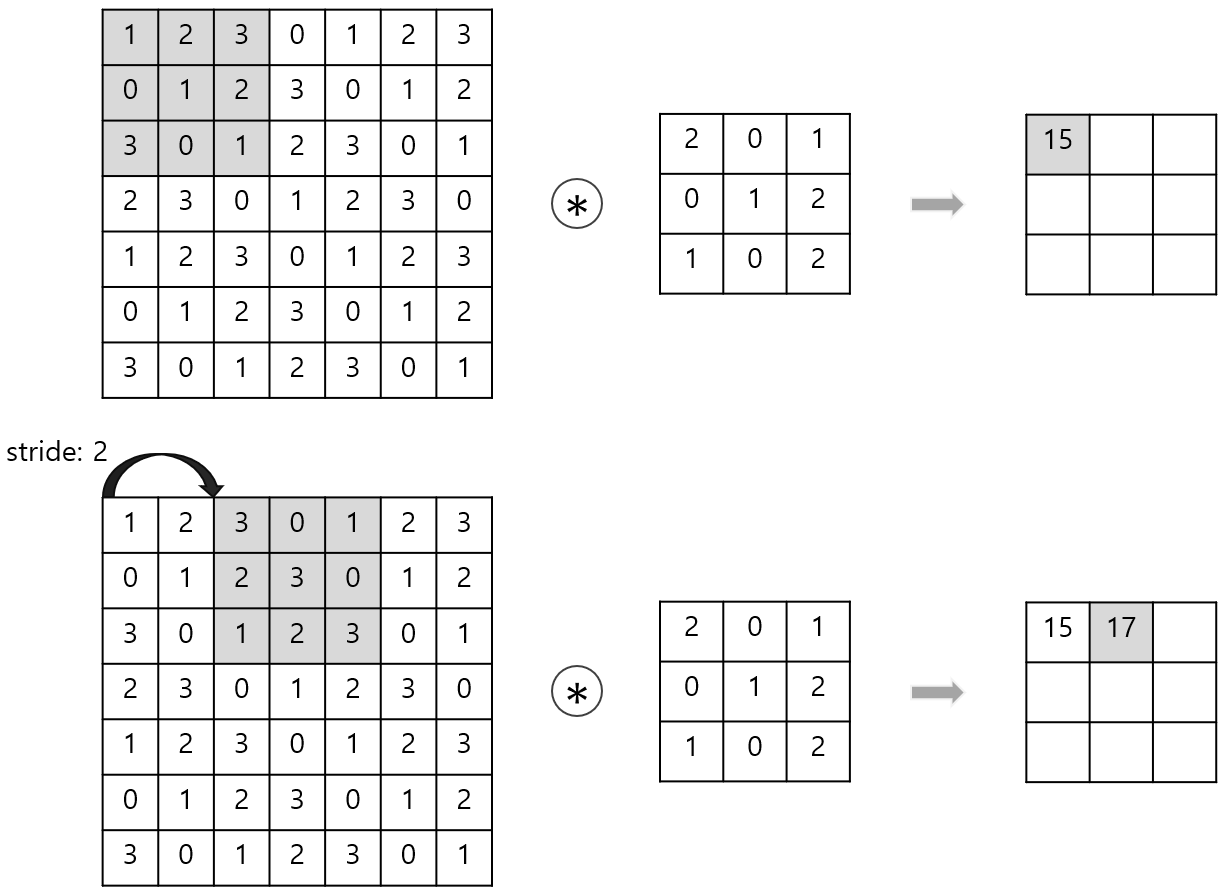
② Stride
- 커널 이동 보폭
- feature map의 크기를 줄이는데에 활용
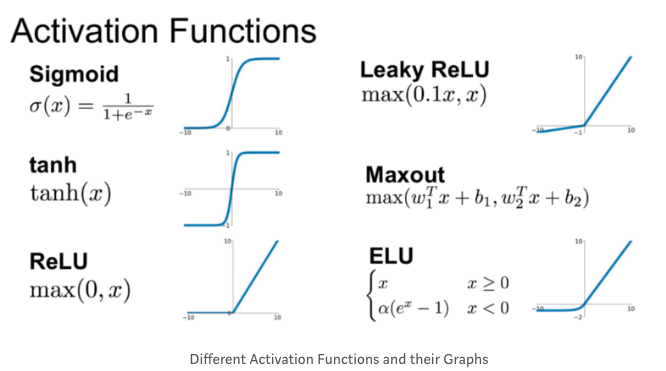
Nonlinear Activation
- XOR 문제을 비롯한 복잡한 문제를 해결하기 위해 필요
- 주로 ReLU를 많이 활용!
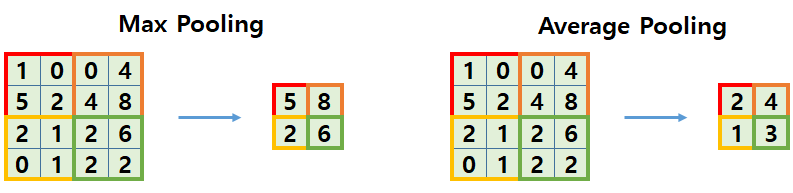
Pooling
- 풀링은 subsampling이라고도 함
- 이미지 데이터의 크기를 줄일 때 사용
- 즉, 학습을 할 때 파라미터의 개수를 줄이기 위해 사용
- 하지만, 풀링을 적용하게 되면 그만큼 일부 에러가 발생할 수 도 있음
- 학습속도를 빠르게 할 수는 있겠지만, 정보가 일부 손실될 수도 있음
- pooling의 종류
- Max pooling (주로 활용!)
- Average pooling
- Stochastic pooling
- 등등
4. CNN 과정 최종 정리
① Input
② Convolution layer blocks
- Convolution with kernel (linear하게 결합)
- (Batch Normalization)
- Nonlinearity(ReLU)
- Pooling(MaxPooling)
③ Output
- Fully Connected Layers
- Softmax(cross-entropy)
'빅데이터 인공지능 > 딥러닝' 카테고리의 다른 글
| [딥러닝] CNN 모델 소개(LeNet, AlexNet, VGG, GoogLeNet, ResNet, DenseNet) (0) | 2022.11.28 |
|---|---|
| [딥러닝] CNN을 위한 PyTorch 구현 (0) | 2022.11.28 |
| [딥러닝] MLP를 위한 PyTorch 구현 (0) | 2022.11.26 |
| [딥러닝] ANN을 위한 PyTorch 구현 (1) | 2022.11.26 |
| [딥러닝] 딥러닝에서의 일반화(Regularization) (0) | 2022.11.25 |
- Total
- Today
- Yesterday
- 자바
- 디프만
- 프론트엔드
- 프론트엔드 기초
- CSS
- TypeScript
- 파이썬
- testing
- Python
- 자바스크립트
- 데이터분석
- 프론트엔드 공부
- jest
- 리액트
- 딥러닝
- JSP
- react-query
- 타입스크립트
- 프로젝트 회고
- 머신러닝
- HTML
- rtl
- 자바스크립트 기초
- 리액트 훅
- 스타일 컴포넌트 styled-components
- react
- 인프런
- next.js
- styled-components
- frontend
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
