티스토리 뷰

▶딥러닝 로지스틱 회귀
우선 로지스틱에 대해 알아보고 코드를 살펴봅시다.
▷선형회귀 vs 로지스틱 회귀

션형 회귀도 로지스틱 회귀 모두 지도학습으로 학습 데이터로부터 x → y의 관계를 설명하는 함수(f)를 찾습니다.
둘의 차이점은 선형 회귀는 출력 변수가 연속형, 로지스틱 회귀는 출력 변수가 범주형이라는 것입니다.

선형회귀와 로지스틱 회귀는 공톡적으로 y값을 잘 예측하는 선형식을 찾는 것이 목표이지만,
이때 로지스틱 회귀는 선형식 중에서도 class1과 class2를 구별하기 위한 판별식을 찾아 새로운 관측치가 왔을 때 이를 기존 범주 중 하나로 예측하게 됩니다.
▷로지스틱 회귀모델의 필요성
나이에 따른 혈압 데이터를 예시로 들어보겠습니다.

만약 위 데이터를 선형 회귀 모델로 만들게 된다면 나이에 따른 특정 혈압 수치를 예측하게 됩니다.
하지만 우리는 특정 수치가 아닌 고혈압/정상/저혈압 여부를 알고 싶기 때문에 y가 범주형인 로지스틱 회귀를 사용하는 것이 적절하겠습니다.
로지스틱 회귀모델을 이용한 사례를 몇 가지 적어보겠습니다.
- 제품이 불량인지 양품인지 분류
- 고객이 이탈 고객인지 잔류 고객인지 분류
- 카드 거래가 정상인지 사기인지 분류
- 내원 고객이 질병이 있는지 없는지 분류
- 이메일이 스팸인지 정상 메일인지 분류
▷이진형 종속변수(y)
이진형 반응변수(y)가 주어진 경우, 설명변수(x)와 반응변수(y)의 관계를 선형으로 나타내는 것은 적합하지 않습니다.
이때 출력값이 0과 1 사이(확률)가 되도록 모델을 구성합니다.
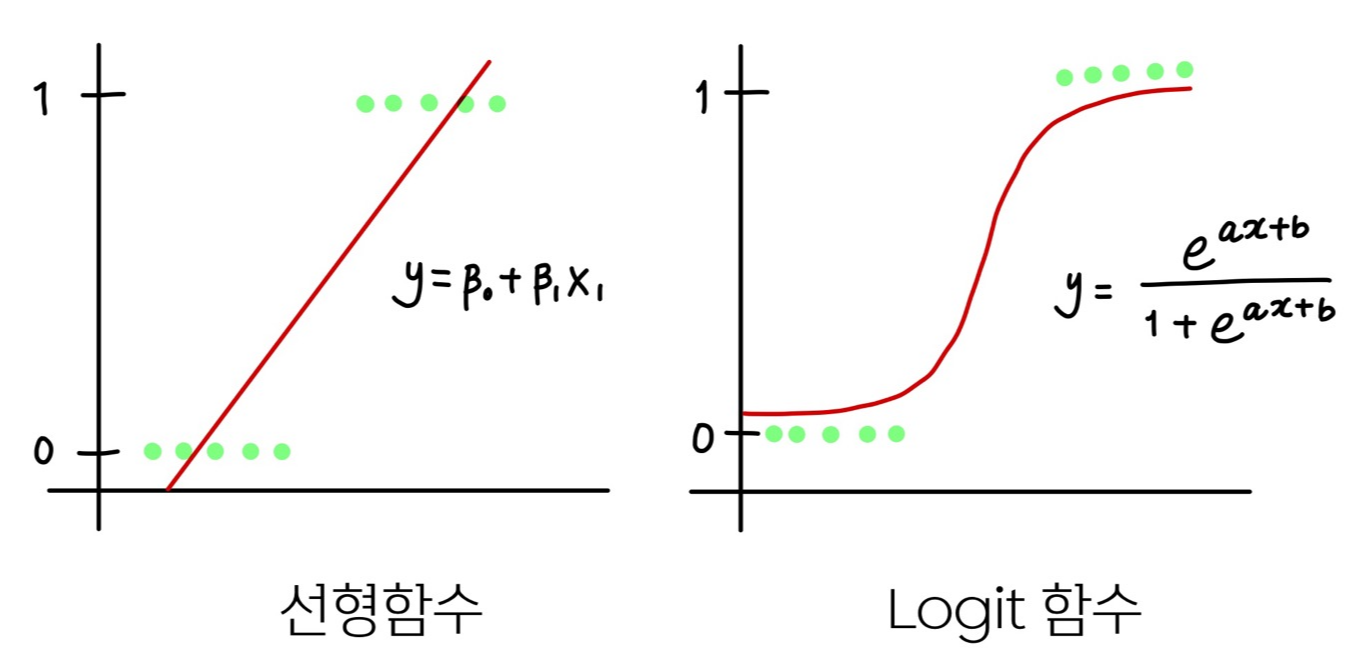
▷시그모이드 함수(Sigmoid Function)
시그모이드 함수는 S자 모양의 함수로 로지스틱 함수, 오차 함수, 정규분포의 cdf, 역 탄젠트 함수 등 다양한 함수에서 사용됩니다.
함수의 출력값은 0에서 1사이의 값을 갖습니다.

시그모이드 함수의 특징은 다음과 같습니다.
- 단조함수(Monotonic function)
- 모든 점에서 미분 가능
- 모든 점에서의 미분 값이 양의 값
- 단 하나의 변곡점
def sigmoid(x):
return 1/(1+np.exp(-x))
▷실습 코드
1) 라이브러리 import
import torch
import torch.nn as nn
import torch.nn.function as F
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
2) 실습에 필요한 데이터셋
# [1, 2]: 1시간 자율학습, 2시간 과외학습 -> [0]: 불합격 / [1]: 합격
# 으로 이해해봅시다.
x_train = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_train = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_train)
y_train = torch.FloatTensor(y_train)print(x_train.shape) # torch.Size([6, 2])
print(y_train.shape) # torch.Size([6, 1])
3) W(가중치)와 b(편향) 초기화
W = torch.zeros((2, 1), requires_grad=True) # 기울기 2개
b = torch.zeors(1, requires_grad=True)
4) 실습1 - 분류 모델 만들기
optimizer = optim.SGD([W, b], lr=0.01)
epoch_count = 1000
for epoch in range(1, epoch_count + 1):
H = torch.sigmoid(x_train.matmul(W) + b)
cost = F.binary_cross_entropy(H, y_train)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if epoch % 100 == 0:
print('Epoch:{:4d}/{} Cost:{:6f}'.format(epoch, epoch_count, cost.item()))out:

최적화를 통해 W와 b를 업데이트 했습니다.
이를 통해 만들어진 H를 출력해보겠습니다.
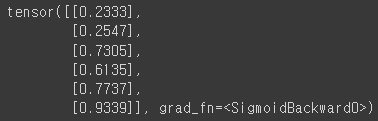
H = torch.sigmoid(x_train.matmul(W) + b)
print(H) # 출력out:

위 출력 값은 각 샘플에 대한 확률을 나타냅니다.
이를 True/False로 출력해봅시다.
pred = H >= torch.FloatTensor([0.5])
print(pred) # 출력out:

5) 실습2 - nn.Module로 구현하기
- nn.Sequential() : nn.Module 레이어를 차례로 찾을 수 있도록 함. 딥러닝 모델을 빠르게 모델링 가능
- 사용하고자 하는 모듈을 입력하면 그 순서대로 모듈을 전달합니다.
model = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid()
)model(x_train) # 만든 모델에 데이터를 넣어줌out:

모델을 출력해보면 포함되어 있는 모듈과 자세하게 그 모듈을 파라미터도 확인할 수 있습니다.
print(model)out:

방금 만든 model을 최적화 해보겠습니다.
epoch_count = 1000
optimizer = optim.SGD(model.parameters(), lr=0.01)
for epoch in range(1, epoch_count + 1):
H = model(x_train)
cost = F.binary_cross_entropy(H, y_train)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if epoch % 10 == 0:
pred = H >= torch.FloatTensor([0.5]) # T/F
cr_pred = pred.float() == y_train # 예측값과 실제값이 맞는지 확인해서 넣기
accuracy = cr_pred.sum().item() / len(cr_pred)
print('Epoch:{:4d}/{} Cost:{:6f} Accuracy"{:2.2f}'.format(epoch, epoch_count, cost.item(), accuracy*100))out:
...

최적화를 완료했으니 업데이트된 H를 출력해봅시다.
model(x_train)out:
자세하게 model의 parameter들이 어떤 값으로 업데이트가 되었는지 출력해봅시다.
print(list(model.parameters()))out:

W(가중치) 2개는 각각 0.7677, -0.6514으로 최종 업데이트가 되었고, b(편향)은 최종적으로 -0.6546으로 업데이트 되었음을 알 수 있습니다.
6) 실습3 - class로 모델 구현하기
신경망 모델을 nn.Module의 하위 클래스로 정의하고, __init__에서 신경망 계층들을 초기화합니다.
nn.Modul을 상속받은 모든 클래스는 forward 메소드에 입력 데이터에 대한 연산들을 구현합니다.
class를 직접 구현해 봅시다.
class BinaryClassifier(nn.Module):
def __init__(self):
super().__init__() # 부모 클래스 호출
self.linear = nn.Linear(2, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
return self.sigmoid(self.linear(x))방금 class를 정의했으니 정의한 class를 통해 모델을 생성합니다.
model = BinaryClassifier()모델 최적화를 진행해 봅시다.
epoch_count = 1000
optimizer = optim.SGD(model.parameters(), lr=0.01)
for epoch in range(1, epoch_count + 1):
H = model(x_train)
cost = F.binary_cross_entropy(H, y_train)
optimizer.zero_grad()
cost.backward()
optimizer.step()
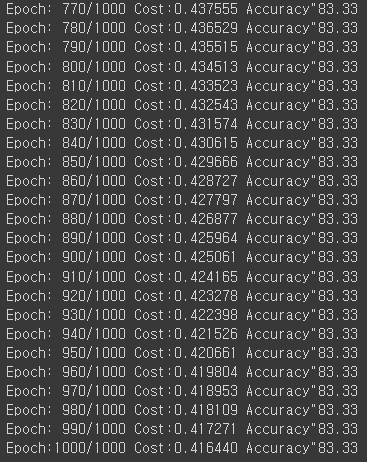
if epoch % 10 == 0:
pred = H >= torch.FloatTensor([0.5]) # T/F
cr_pred = pred.float() == y_train # 예측값과 실제값이 맞는지 확인해서 넣기
accuracy = cr_pred.sum().item() / len(cr_pred)
print('Epoch:{:4d}/{} Cost:{:6f} Accuracy"{:2.2f}'.format(epoch, epoch_count, cost.item(), accuracy*100))out:
최적화를 통헤 model의 W(가중치)와 b(편향) 업데이트를 완료했습니다.
임의의 샘플을 넣어 예측 결과를 출력해 보겠습니다.
val = torch.FloatTensr([2, 2]) # 2시간 자율학습, 2시간 과외학습을 했을 때
pred = model(val)
print('학습 후 입력이 2, 2 일 때 합격 여부: ', pred)out:

합격할 확률이 0.3789로 예측되었습니다.
한번 더 예측 결과를 출력해 보겠습니다.
val = torch.TensorFloat([5, 4]) # 5시간 자율학습, 4시간 과외학습 했을 때
pred = model(val)
print('학습 후 입력이 5, 4일 때 합격 여부: ', pred)out:

합격할 확률이 0.6874로 예측되었습니다.

여기까지 딥러닝 로지스틱 회귀에 대해 알아보았습니다.
nn.Sequential()을 이용하면 빠르게 모델링을 할 수 있겠습니다 :)
'빅데이터 인공지능 > 딥러닝' 카테고리의 다른 글
| [딥러닝] 역전파(Backpropagation) - 경사하강법 & 활성화 함수 (0) | 2022.09.12 |
|---|---|
| [딥러닝] 파이토치(PyTorch)로 모델 구현 실습🎯- MNIST 손글씨 데이터셋 (2) | 2022.09.03 |
| [딥러닝] 다중선형회귀(Multi Linear Regression) (0) | 2022.08.30 |
| [딥러닝] 선형 회귀(Linear Regression) (0) | 2022.08.29 |
| [딥러닝] 딥러닝의 이해 (0) | 2022.08.29 |
- Total
- Today
- Yesterday
- 파이썬
- 머신러닝
- frontend
- next.js
- 프론트엔드 기초
- TypeScript
- 디프만
- 리액트 훅
- 프론트엔드
- react-query
- rtl
- 데이터분석
- HTML
- 프론트엔드 공부
- styled-components
- 자바
- CSS
- 리액트
- react
- JSP
- 자바스크립트 기초
- 프로젝트 회고
- 스타일 컴포넌트 styled-components
- 타입스크립트
- testing
- Python
- 인프런
- jest
- 딥러닝
- 자바스크립트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
