티스토리 뷰

▶딥러닝 다중선형회귀
앞서 X와 Y가 하나씩 존재하는 선형회귀에 대해 공부해 보았습니다.
이번에는 X변수가 여러 개인 다중 선형회귀에 대해서 알아보겠습니다.
다중선형회귀는 여러 개의 특성을 이용해 종속변수를 예측하기 때문에 일반 선형회귀보다 더 좋은 성능을 기대할 수 있습니다.
다음 데이터를 참고해서 다중 선형회귀 실습을 해보겠습니다.
| 공부한 시간 | 2 | 2 | 2 | 3 | 4 | 4 |
| 학원에서 공부한 시간 | 0 | 1 | 2 | 1 | 1 | 2 |
| 과외로 공부한 시간 | 0 | 0 | 1 | 1 | 2 | 2 |
| 점수 | 50 | 60 | 65 | 70 | 75 | 85 |
위 데이터를 참고한 퍼셉트론 그림은 다음과 같습니다.

▷라이브러리 import
import torch
import torch.nn as nn
import torch.nn.function as F
import torch.optim as optim
▷데이터셋
x1_train = torch.FloatTensor([[2], [2], [2], [3], [4], [4]])
x2_train = torch.FloatTensor([[0], [1], [2], [1], [1], [2]])
x3_train = torch.FloatTensor([[0], [0], [1], [1], [2], [2]])
y_train = torch.FloatTensor([[50], [60], [65], [70], [75], [85]])
▷구현1 - 가중치 각각을
W1 = torch.zeros(1, requires_grad=True)
W2 = torch.zeros(1, requires_grad=True)
W3 = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
optimizer = optim.SGD([W1, W2, W3, b], lr=1e-5)
tot_epochs = 100000
for epoch in range(1, tot_epochs+1):
H = x1_train*W1 + x2_train*W2 + x3_train*W3 + b
cost = torch.mean((H - y_train) ** 2)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if epoch % 1000 == 0:
print('Epoch {:4d}/{} W1:{:.3f} W2:{:.3f} W3:{:.3f} b:{:.3f} Cost:{:.6f}'.format(epoch, tot_epochs, \
W1.item(), W2.item(), W3.item(), b.item(), cost.item()))out:
...

위 코드는 가중치를 3개로 그대로 두고 업데이트를 했습니다.
이제는 가중치를 묶어서 행렬곱을 이용하는 방법으로 구현해보겠습니다.
▷구현2 - 가중치를 한번에 행렬곱으로
구현1에서 사용했던 데이터는 아래와 같습니다.
x1, x2, x3를 따로따로 만들었었습니다.
x1_train = torch.FloatTensor([[2], [2], [2], [3], [4], [4]])
x2_train = torch.FloatTensor([[0], [1], [2], [1], [1], [2]])
x3_train = torch.FloatTensor([[0], [0], [1], [1], [2], [2]])
y_train = torch.FloatTensor([[50], [60], [65], [70], [75], [85]])이제는 각각 y에 해당하는 x 데이터들을 하나씩 묶어 데이터셋을 구성합니다.
x_train = torch.FloatTensor([[2, 0, 0], [2, 1, 0], [2, 2, 1], [3, 1, 1], [4, 1, 2], [4, 2, 2]])
y_train = torch.FloatTensor([[50], [60], [65], [70], [75], [85]])데이터 shape을 확인해봅시다.
print(x_train.shape) # torch.Size([6, 3])
print(y_train.shape) # torch.Size([6, 1])가중치도 한번에 묶어서 정의할 겁니다.
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)이제 본격적으로 구현해봅시다.
선형식이 y = x * W + b 였습니다.
주목할 점은 x * W 부분인데, x_train의 shape은 [6, 3] 이고 W의 shape은 [3, 1]이므로 행렬곱이 가능하다는 점입니다.
optimizer = optim.SGD([W, b], lr=1e-5)
tot_epochs=100000
for epoch in range(1, tot_epochs+1):
H = x_train.matmul(W) + b # matmul: 행렬곱
cost = torch.mean((H - y_train) ** 2)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if epoch % 1000 == 0:
print('Epoch {:4d}/{} H:{} Cost:{:.6f}'.format(epoch, tot_epochs, H.squeeze().detach(), cost.item()))out:
...

▷배치(Batch)
배치는 전체 데이터를 작은 단위로 나눠서 해당 단위로 학습하는 개념입니다.
배치 학습을 하게 되면 배치만큼만 가져와서 배치에 대한 비용(cost)를 계산하고 경사하강법을 수행합니다.
배치를 가져와서 경사 하강법을 수행하고 마지막 배치까지 이를 반복하게 되는데 전체 데이터에 대한 학습이 모두 끝나면 1에폭이 끝나게 됩니다.
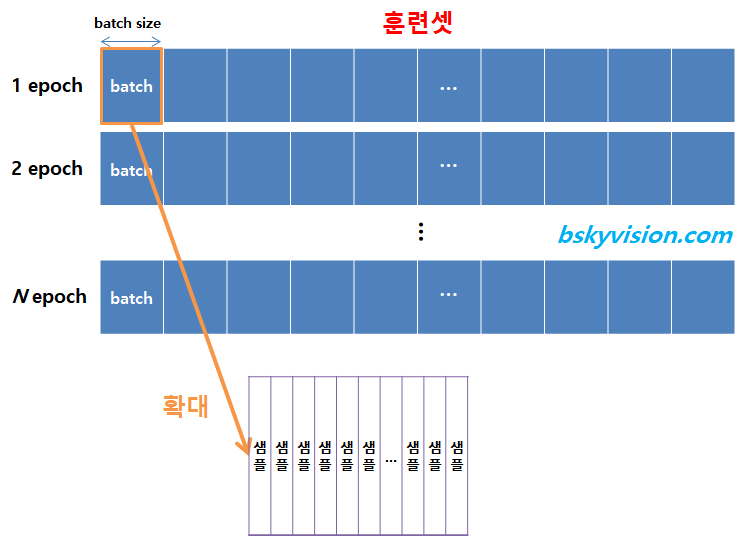
배치 하나를 미니배치(Minibatch)라고 합니다.
배치 크기(batch size)는 보통 2의 제곱수를 사용합니다.
이유는 CPU와 GPU의 메모리가 2의 배수이므로 배치 크기가 2의 제곱수일 경우 데이터의 송수신이 효율적이기 때문입니다.
배치 사이즈와 관련된 예시를 하나 들어보자면...
총 1,000개의 훈련 샘플이 있는데, 배치 사이즈가 20이라면 20개의 샘플 단위마다 모델의 가중치를 한 번씩 업데이트가 일어납니다.
즉 1에폭 동안 50번의 가중치 업데이트가 일어난다는 말이 되겠습니다.
이때 total 에폭이 10이라면, 가중치를 50번 업데이트 하는 것을 10번 반복한다는 뜻이므로 결국 10*50 = 500번의 가중치 업데이트가 일어납니다.
▷데이터로더(Data Loader)
데이터로더는 데이터를 좀 더 쉽게 나눌 수 있도록 도와주는 파이토치 및 텐서플로우에서 제공하는 라이브러리입니다.
또한 데이터셋도 제공하기 때문에 배치 학습, 데이터 사용, 병렬 처리 등을 간단하게 수행 가능하게 해줍니다.
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoaderTensorDataset을 통해 데이터셋을 만들어주고, DataLoader를 통해 편하게 배치를 할당하겠습니다.
dataset = TensorDataset(x_train, y_train)
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)이제 구현을 해봅시다.
model = nn.Linear(3, 1) # 입력 3개 받아서 1개 출력
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5)
epoch_count=5000
for epoch in range(epoch_count + 1):
for batch_idx, datas in enumerate(dataloader):
x_train, y_train = datas
H = model(x_train)
cost = F.mse_loss(H, y_train)
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch:{:4d}/{} Batch:{}/{} Cost:{:.6f}'.format(epoch, epoch_count, batch_idx+1, len(dataloader), cost.item()))out:
...
가중치와 편향 업데이트가 끝났으므로 이제 모델을 확인해 보겠습니다.
val = torch.FloatTensor([[5, 2, 3]])
pred = model(val)
print('학습 후 입력이 5, 2, 3일 때 예측 값: ', pred)out:

최종적으로 업데이트된 가중치와 편향도 확인해 봅시다.
print(list(model.parameters()))out:


여기까지 딥러닝 다중선형회귀에 대해 알아보았습니다 :)
'빅데이터 인공지능 > 딥러닝' 카테고리의 다른 글
| [딥러닝] 역전파(Backpropagation) - 경사하강법 & 활성화 함수 (0) | 2022.09.12 |
|---|---|
| [딥러닝] 파이토치(PyTorch)로 모델 구현 실습🎯- MNIST 손글씨 데이터셋 (2) | 2022.09.03 |
| [딥러닝] 로지스틱 회귀(Logistic Regression) 개념부터 실습까지 (0) | 2022.09.03 |
| [딥러닝] 선형 회귀(Linear Regression) (0) | 2022.08.29 |
| [딥러닝] 딥러닝의 이해 (0) | 2022.08.29 |
- Total
- Today
- Yesterday
- frontend
- 자바스크립트
- Python
- 프론트엔드 공부
- 자바
- next.js
- TypeScript
- 딥러닝
- 파이썬
- rtl
- 머신러닝
- HTML
- 프로젝트 회고
- react-query
- JSP
- 자바스크립트 기초
- CSS
- styled-components
- 데이터분석
- react
- 스타일 컴포넌트 styled-components
- 프론트엔드
- jest
- 디프만
- 프론트엔드 기초
- 타입스크립트
- testing
- 리액트 훅
- 리액트
- 인프런
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
