티스토리 뷰

▶ 딥러닝에서의 최적화
이번 글에서는 이전 글에서 언급된 Gradient Descent와 Regularization 기법에 대해 알아보려고 합니다 :)
0. 최적화 개념
최적화(Optimization)
딥러닝 분야에서 최적화(Optimization)란 손실 함수(Loss Function) 값을 최소화 하는 파라미터를 구하는 과정입니다.
딥러닝에서는 학습 데이터를 입력하여 네트워크 구조를 거쳐 예측값을 얻습니다.
이 예측값과 실제 정답과의 차이를 비교하는 함수가 손실 함수(Loss Function)입니다.
즉, 모델이 예측한 값과 실제값의 차이를 최소화하는 네트워크 구조의 파라미터(Feature)를 찾는 과정이 최적화입니다.
최적화 기법에는 여러 가지가 있으며, 잠시후 살펴봅시다.
1. Gradient Descent(경사 하강법)
- Gradient Descent 알고리즘들
- Batch gradient descent
- Stochastic gradient descent
- Mini-batch gradient descent
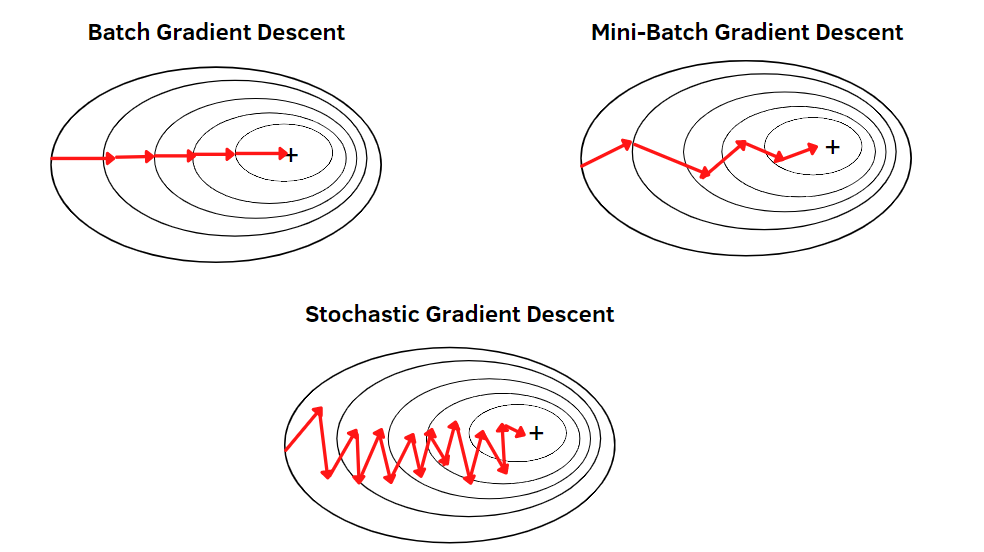
① Batch gradient descent(배치 경사 하강법)
Batch gradient descent 에서 Batch는 데이터를 분할한다는 개념이 아닌, 전체 훈련 데이터셋을 의미합니다.
Batch gradient descent는 전체 데이터셋에 대해서 오차를 구하고 기울기를 한번만 계산하는 방법입니다.
배치 경사 하강법의 특징
- 한 스텝에 전체 데이터를 사용하기 때문에 연산 횟수가 적습니다.(1 에포크 당 1회 업데이트)
- 연산 횟수는 적지만 학습 속도는 매우 느려질 수 있어서 큰 데이터에는 적합 X
- 최적해에 대한 수렴이 안정적으로 진행
- 하지만, local optimal 상태가 되면 빠져나오기 어려움
- weight 업데이트를 위해 모든 학습 데이터에 대해 저장해야 하므로 데이터가 큰 경우 전체 데이터를 못 읽거나 많은 메모리가 필요함
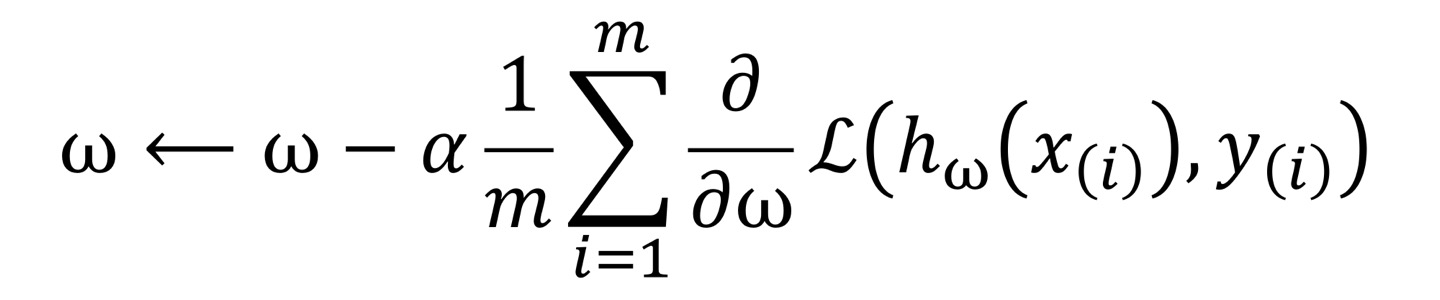
배치 경사 하강법 훈련 과정
1. weight에 대해 랜덤하게 초기화
2. 수렴이 될 때까지 다음을 반복
- 모든 데이터에 대한 weight를 계산
- weight가 업데이트 되는 방향으로 적용
3. loss가 최소가 되는 weight를 도출
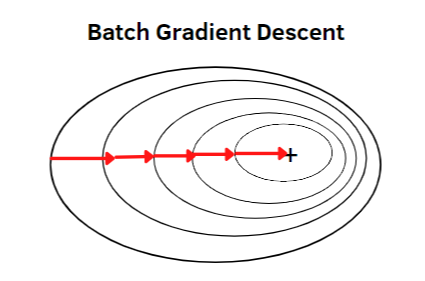
위 그림에서 같은 줄에 대해서는 모두 같은 loss를 가지고 있는데,
Batch gradient descent는 loss function을 미분한 기울기에 수직인 방향으로 작동이 되는 것을 확인할 수 있습니다.
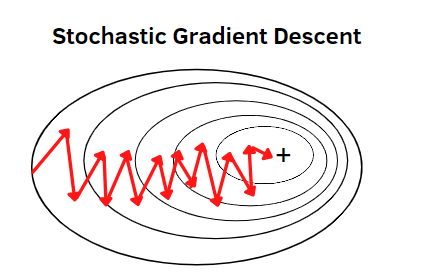
② Stochastic gradient descent(확률적 경사 하강법)
확률적 경사 하강법은 무작위로 한 개의 샘플 데이터셋을 추출해 그 샘플에 대해서만 기울기를 계산하는 방법입니다.
따라서 추출된 데이터 한 개에 대해서 오차를 계산하고 Gradient descent 알고리즘을 적용하게 됩니다.
확률적 경사 하강법의 특징
- 오로지 랜덤하게 추출된 샘플 데이터셋에 대해서만 경사를 계산하므로 매 반복마다 다뤄야 할 데이터가 줄어들게 되어 학습 속도가 빨라지게 됨
- 같은 이유로 메모리 소모량이 매우 낮으며, 큰 데이터셋이라 할지라도 학습이 가능
- 학습 중간 과정에서 진폭이 크고 배치 경사 하강법보다 불안정하게 움직임
- 데이터를 하나씩 처리하기 때문에 오차율이 크고, GPU의 성능을 전부 활용할 수 없음
- 손실 함수가 최솟값에 가는 과정이 불안정하다 보니 최적해(global minimum)에 정확히 도달하지 못할 가능성이 있음
- 배치 경사 하강법과 반대로 local minimum에 빠지더라도 쉽게 빠져나올 수 있음
확률적 경사 하강법 훈련 과정
1. weight에 대해서 랜덤하게 초기화
2. 수렴될 때까지 다음을 반복
- 싱글 데이터 포인트를 랜덤하게 선택
- 위 포인트에 대해 gradient 계산
- gradient를 바탕으로 weight를 계산
3. 최적의 weight를 반환
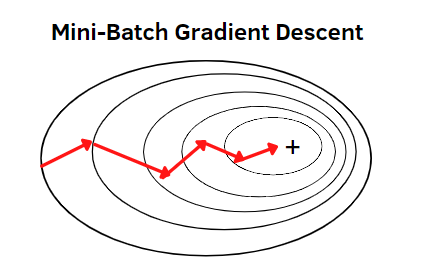
③ Mini-batch gradient descent(미니 배치 경사 하강법)
전체 데이터를 batch_size개씩 나눠 배치로 학습 시키는 방법입니다.
이때 batch_size, 즉 몇개씩 묶어서 gradient를 계산할지는 사용자가 지정합니다.
예를 들어 1,000개인 학습 데이터셋에서 batch_size를 100으로 잡았다면 총 10개의 mini batch가 나오게 됩니다.
즉, 1 에포크 당 10번 gradient를 계산하고 weight를 업데이트하게 됩니다.
미니 배치 경사 하강법의 특징
- 배치 경사 하강법보다 local optimal에 빠질 위험이 적음
- 확률적 경사 하강법보다는 GPU 성능을 활용한 병렬처리가 가능하여 속도면에서 유리
- 전체 데이터가 아닌 일부 데이터만 메모리에 적재하여 사용하므로, 메모리 사용측면에서도 배치 경사 하강법보다 원할
Batch Size 정하기
Batch size는 보통 2의 n승으로 지정한다.
또한, 가능하면 학습데이터 갯수에 나누어 떨어지도록 지정하는 것이 좋은데, 마지막 남은 배치가 다른 사이즈이면 해당 배치의 데이터가 학습에 더 큰 비중을 갖게 되기 때문이다.
그렇기 때문에 보통 마지막 배치의 사이즈가 다를 경우 이는 버리는 방법을 사용한다.
미니 배치 경사 하강법 훈련 과정
1. weight에 대해서 랜덤하게 초기화
2. 수렴될 때까지 다음을 반복
- 사용자가 정한 mini batch 개수만큼의 데이터 포인트를 바탕으로 weight를 업데이트
- mini batch 개수의 데이터를 바탕으로 gradient를 계산
- weight를 업데이트
3. 최적의 weight를 추출
2. Gradient Descent의 한계점
- Vanishing Gradient Problem
- Set th learning rate
- learning rate를 어떻게 설정해주느냐에 따라 학습시 많이 달라져서 적절한 learning rate를 구하는 것이 어려움
① Vanishing Gradient Problem
- sigmoid activation function을 활용했을 때 network layer가 많이 쌓일수록 input에 가까운 layer의 weight의 gradient가 0에 가까워지는 문제
- 이럴 경우 weight가 업데이트 되지 못함
- 이러한 문제를 극복하기 위해, sigmoid가 아닌 다른 형태의 activation function을 활용!
- 주로 ReLU(Rectified Linear Unit) 함수를 사용하게 됨
- 0보다 작은 값을 넣게 되면 0을, 0보다 큰 값을 넣게 되면 그 해당 값이 도출되게 하는 함수
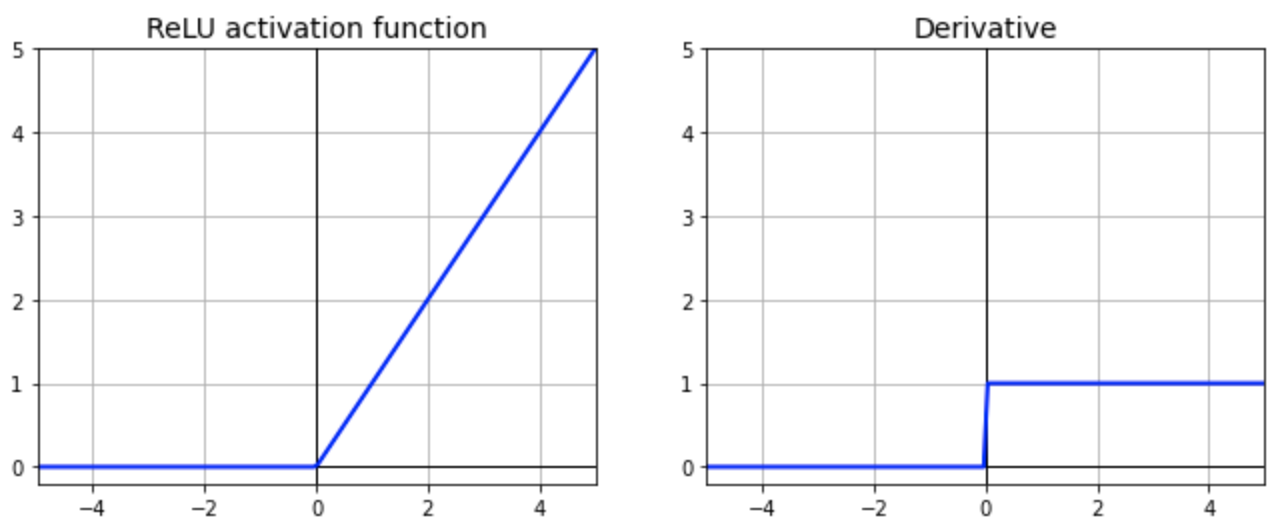
오른쪽 그림을 보면...
아무리 layer의 깊이가 깊어지더라도 weight를 업데이트할 때 gradient가 0보다 클 때는 1이 도출되게 되면서 weigh가 소멸되지 않고 최적의 loss에 가까워지는 형태로 이어질 것입니다.
왼쪽 그림을 보았을 때 드는 의문점은
0일 때는 미분 불가능 하지 않나...?
실제로 neural network를 설계를 해서 학습을 할 때 정확하게 0에 도달하는 값을 얼마나 자주 볼 수 있을까..하기도 하며
정말로 0이 나오게 되는 경우를 위해 error term을 추가하여 0이 도출되지 않도록 하는 방법을 사용하기도 합니다.
② Set the learning rate
- learning rate를 어떻게 적용할 것인가, 어느 learning rate가 가장 적절한가
- learning rate를 설정하는 방법
- 시행 착오
- 다양한 learning rate를 적용해 보면서 가장 잘맞는 learning rate를 찾아서 최종적으로 적용
- Adaptive learning rate
- feature들의 중요성에 맞게, 각 feature(파라미터)마다 다른 learning rate를 적용
- 시행 착오
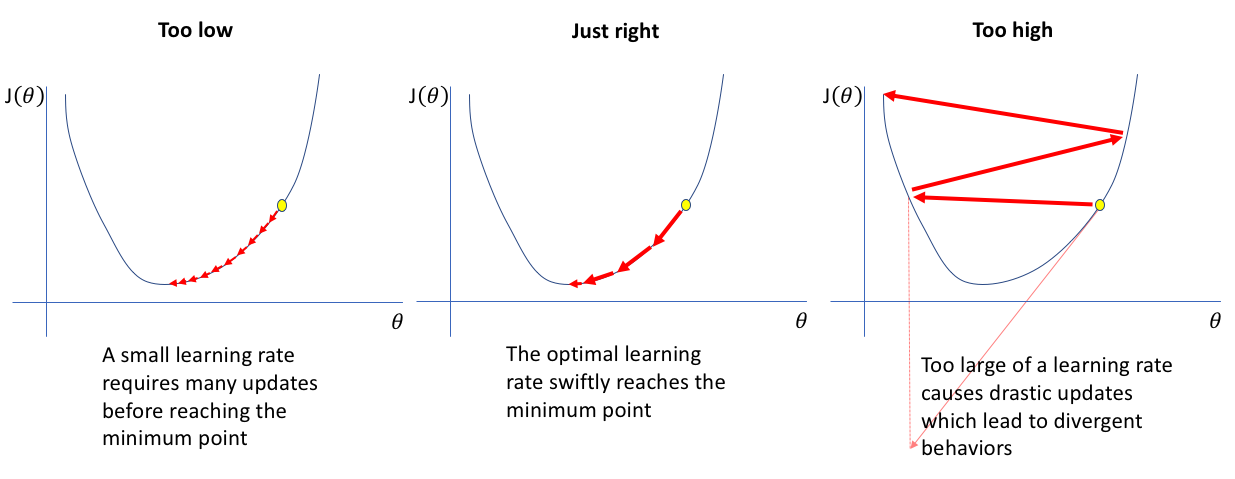
왜 Adaptive learning rate가 효과적인가?
feature들이 모두 동일한 중요도를 갖는 것은 아니기 때문에, feature들의 중요성에 맞게 learing rate를 변형하는 adaptive learing rate를 적용하는 것이 효과적일 수 있습니다.
Adaptive learning rate의 강점
1. 훈련 속도를 가속화
2. learning rate 및 learning rate schedule을 선택해야 하는 부담을 일부 완화할 수 있음
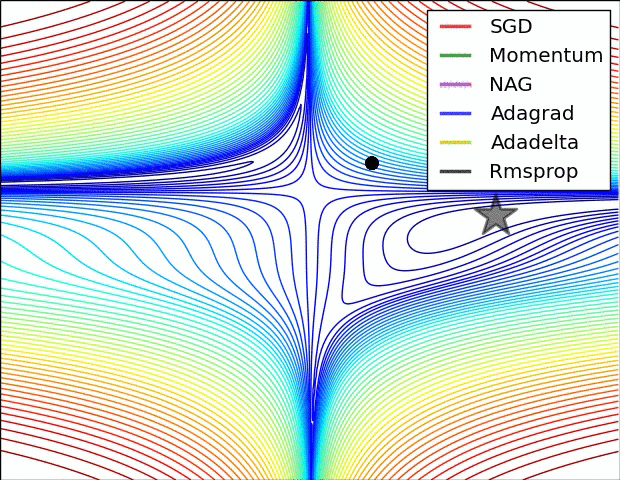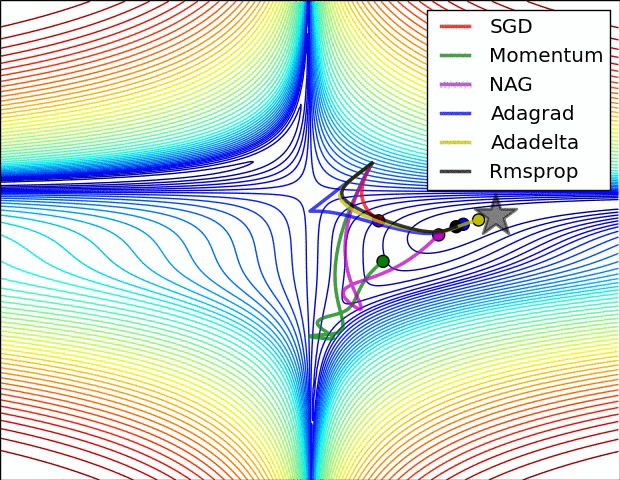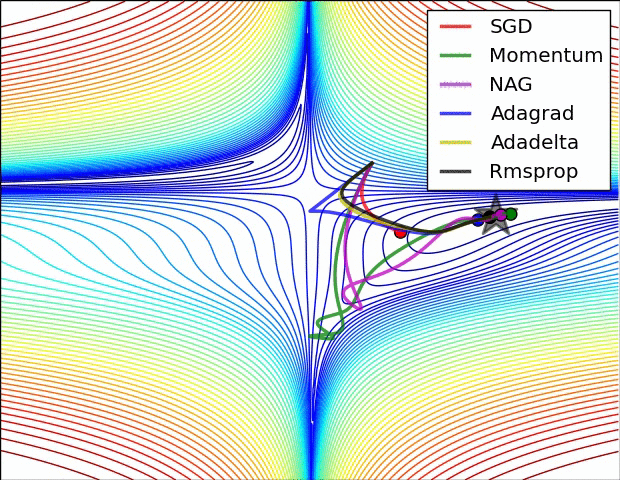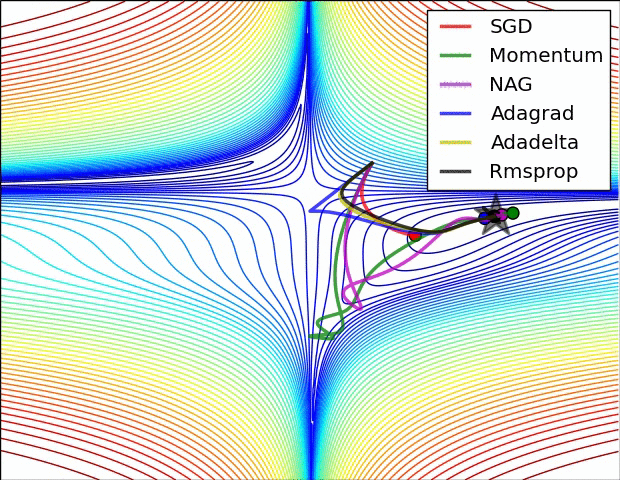
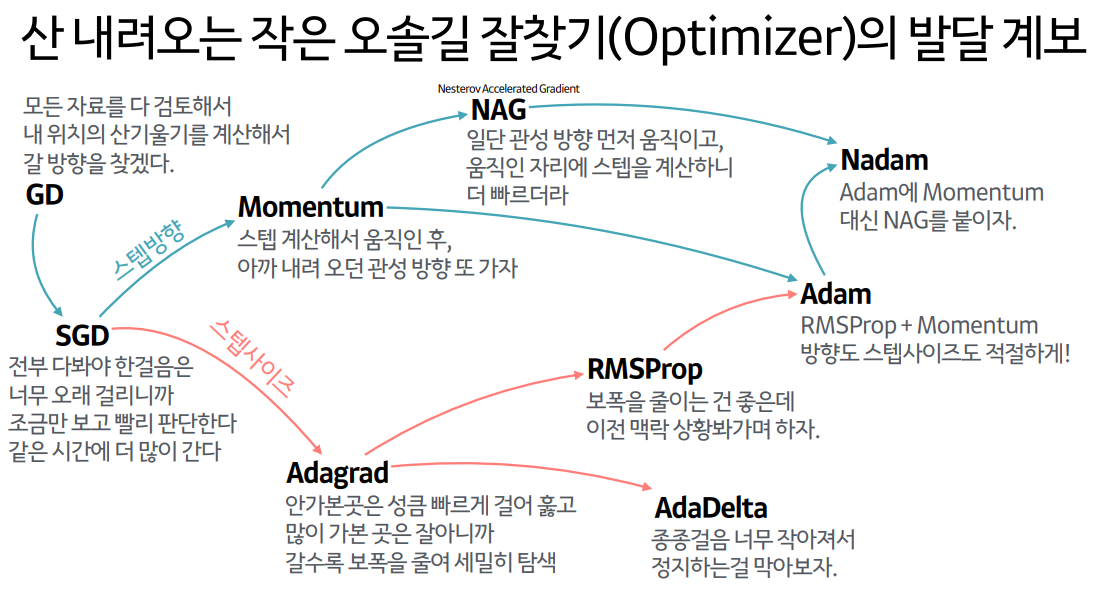
+ Adagrad (Adaptive Gradient)

다음과 같이 learning rate에 적용한 식으로 weight를 업데이트하게 됩니다.
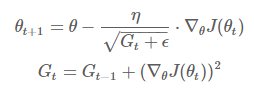
하지만, 스텝이 진행될 수록 G_t가 무한대로 발산하여 스텝 사이즈가 0으로 수렴하는 문제가 발생합니다.
→ weight가 제대로 업데이트 되지 못함 → 이를 해결하는 방법이 RMSProp
+ 그 외 Adaptive Gradient 알고리즘들
- Momentum, Adagrad, RMSProp, Adadelta, Adam, RAdam
'빅데이터 인공지능 > 딥러닝' 카테고리의 다른 글
| [딥러닝] ANN을 위한 PyTorch 구현 (1) | 2022.11.26 |
|---|---|
| [딥러닝] 딥러닝에서의 일반화(Regularization) (0) | 2022.11.25 |
| [딥러닝] MLP(Multi-Layer Perceptron) A to Z (0) | 2022.11.25 |
| [딥러닝] CNN(Convolutional Neural Network)과 MLP(Multi Layer Perceptron) 의 차이 (0) | 2022.11.19 |
| [딥러닝] 딥러닝(ANN, DNN, CNN, RNN, SLP, MLP) 비교 (0) | 2022.11.19 |
- Total
- Today
- Yesterday
- TypeScript
- rtl
- react-query
- 스타일 컴포넌트 styled-components
- JSP
- next.js
- 자바
- 머신러닝
- 자바스크립트
- frontend
- 파이썬
- 프론트엔드 기초
- testing
- CSS
- HTML
- 리액트 훅
- 자바스크립트 기초
- 타입스크립트
- 프로젝트 회고
- 딥러닝
- 디프만
- 리액트
- Python
- 프론트엔드 공부
- 프론트엔드
- 인프런
- jest
- styled-components
- 데이터분석
- react
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
