티스토리 뷰

▶ MLP(Multi-Layer Perceptron) A to Z
이번 글에서는 MLP가 등장하게 된 배경부터 학습하는 방법까지 알아보려고 합니다 :)
1. Deep Learning
- Perceptron
- 딥러닝의 시작 개념
- classification의 알고리즘 중 하나
- 구조적인 building blocks로 이루어져 있음
- 비선형 활성화 함수를 사용
- XOR문제를 풀 수가 없음
- Neural Networks
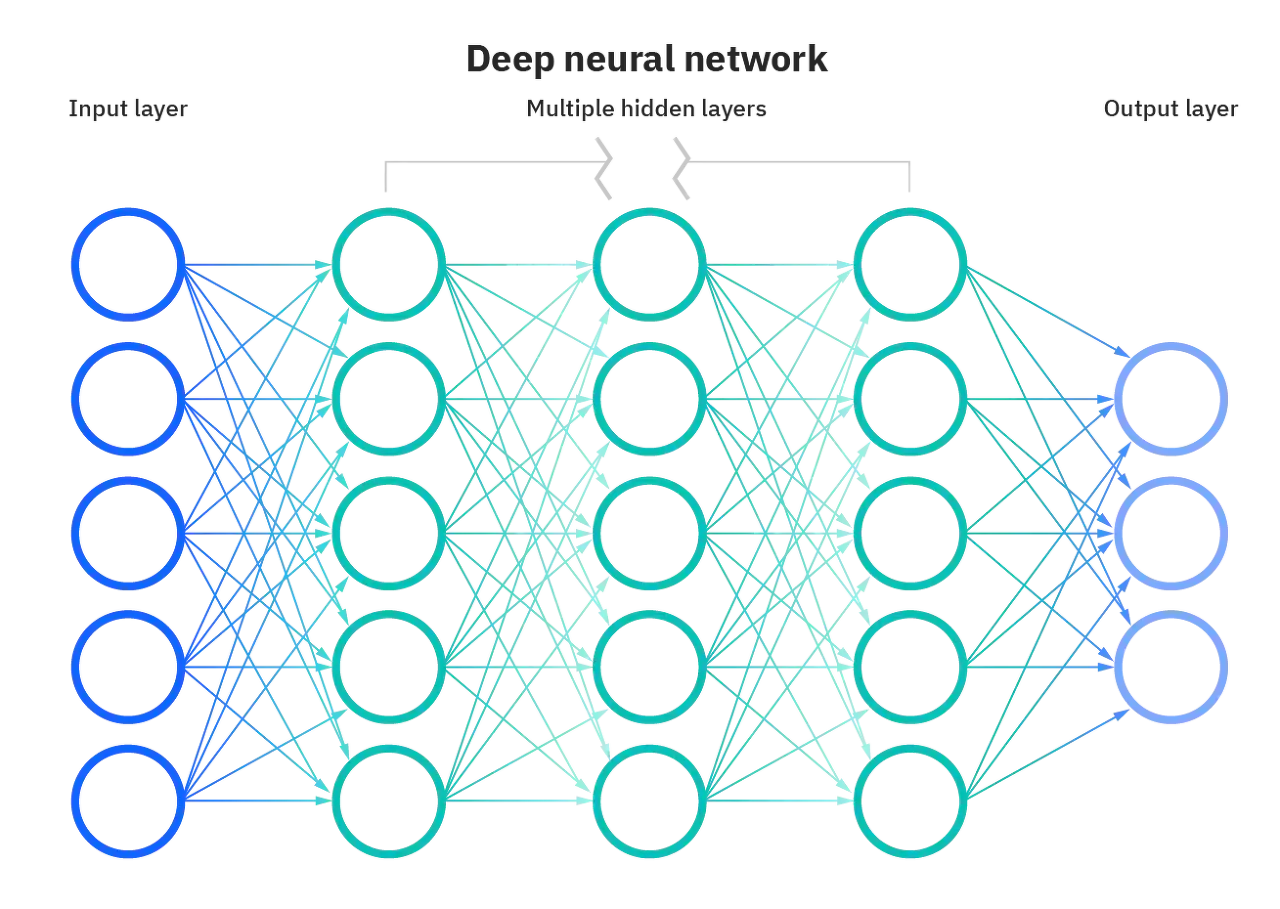
- multi-layer perceptron
- 뉴럴 네트워크를 형성하기 위해 퍼셉트론을 쌓는 것
- backpropagation을 통해 최적화(optimization)
- layer마다 도출해야 하는 weight들을 backpropagation으로 탐색
2. Perceptron
- 퍼셉트론은 forward propagation이다.
- 분류(classification) 알고리즘 중 하나
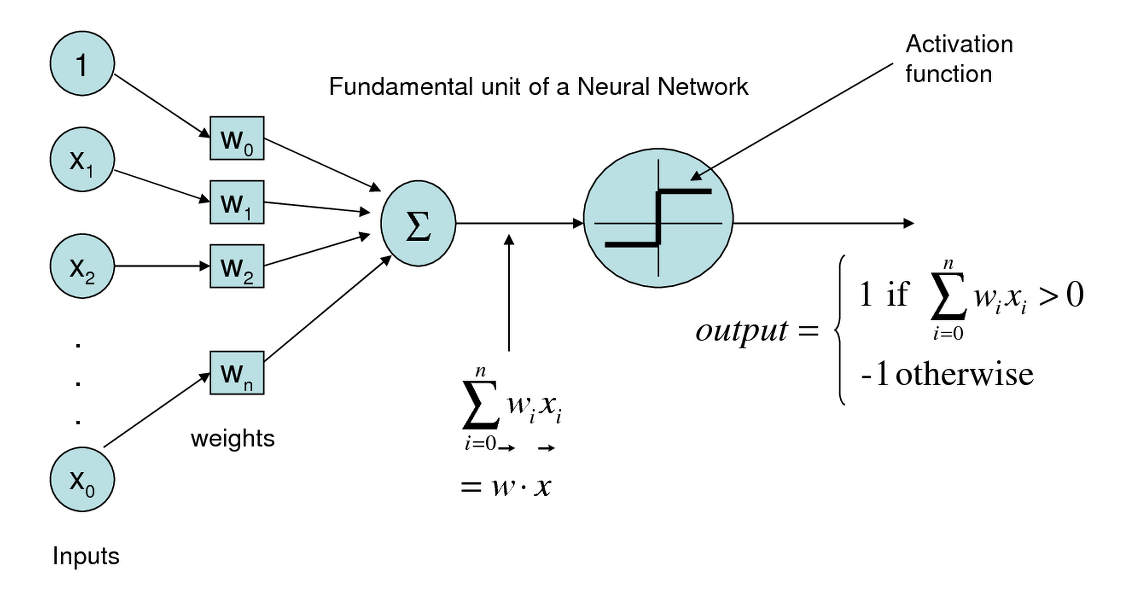
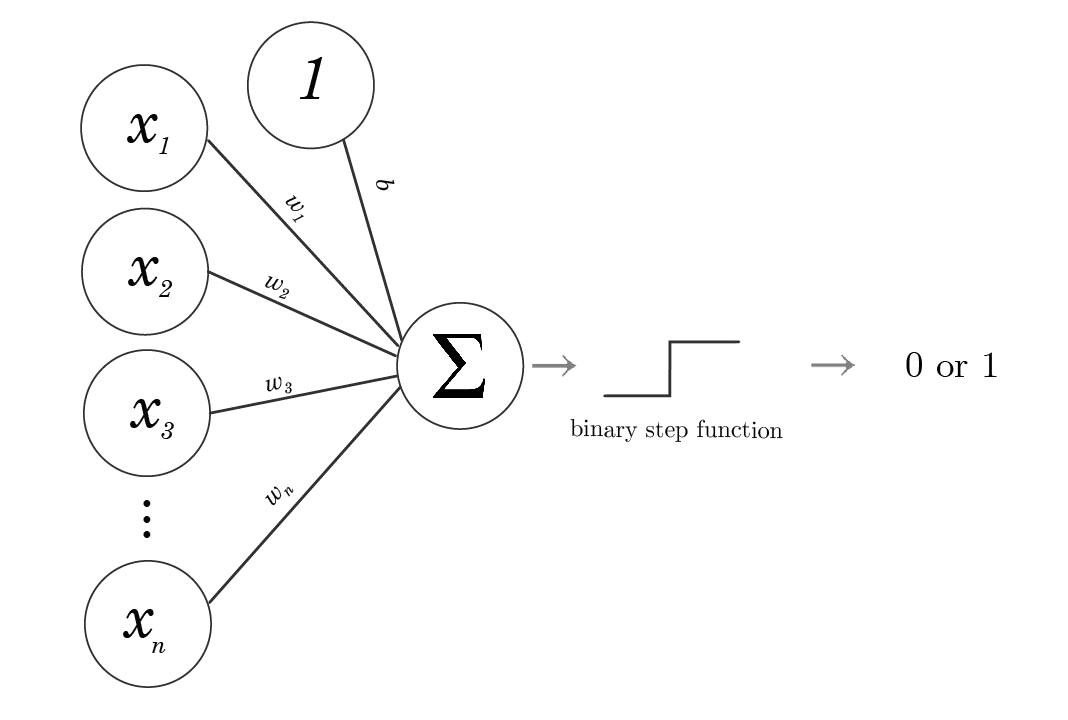
input 데이터가 있고 각각의 데이터에 해당하는 weight가 있어서 주어진 input 데이터와 weight를 결합(연산)해서 그 값이 일정 thresholds를 넘느냐 넘지 않느냐로 분류하는 과정입니다.
이때 데이터와 가중치에 대한 결합을 sign(x)(step function)을 바탕으로 perceptron을 정의할 수가 있는데요.
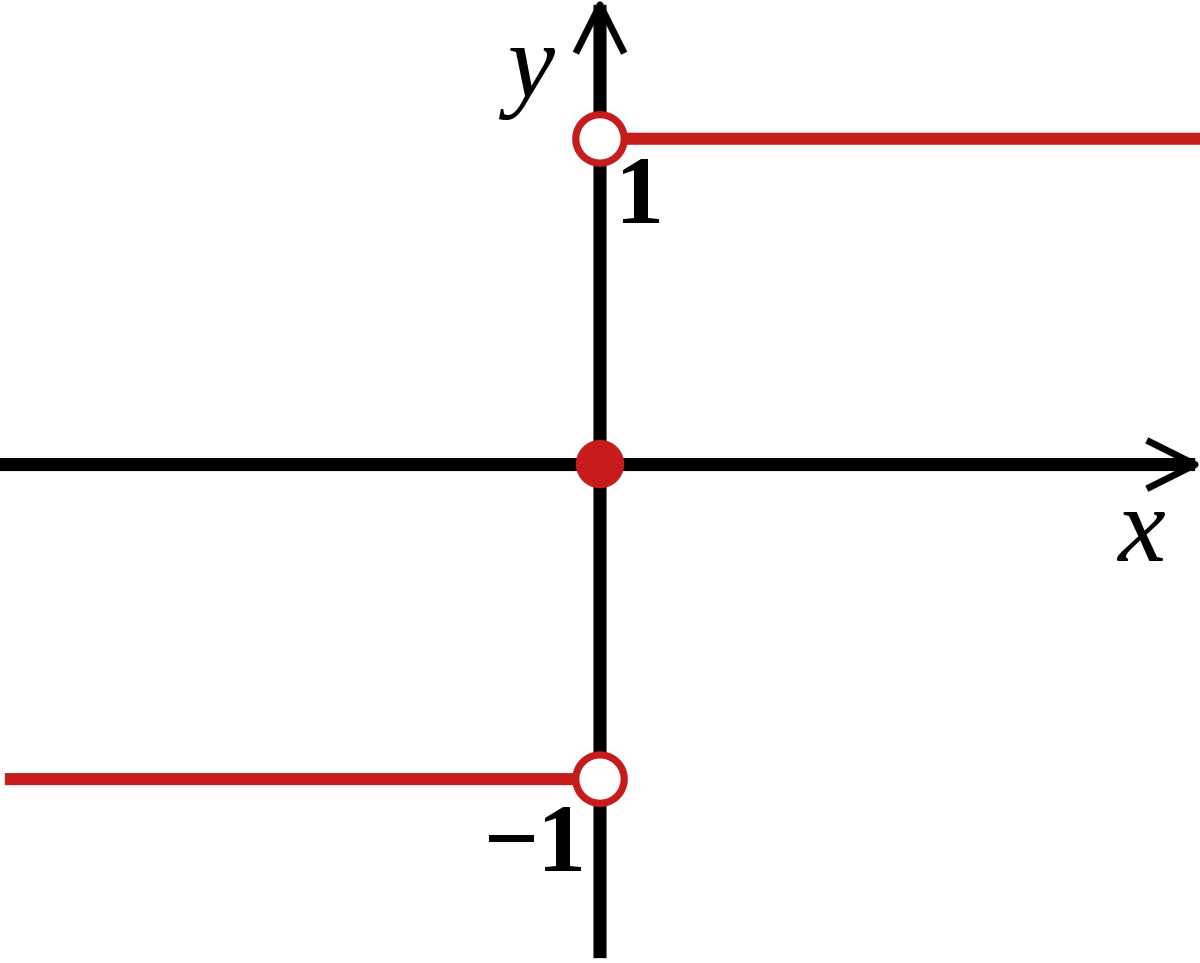
위 sign 함수는 연산하여 얻은 값이 0보다 크면 1을 도출, 0보다 작으면 -1을 도출하게 됩니다.
- 퍼셉트론 예시
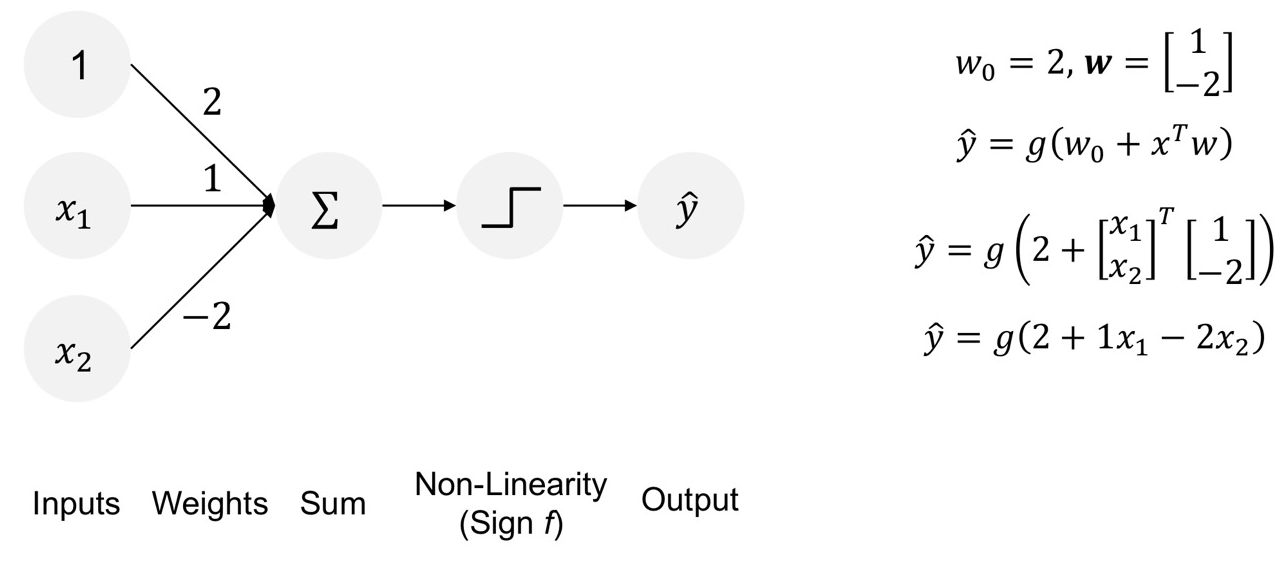
bias와 weight가 주어진 상황에서 bias는 1과 연산되고 input 데이터와 weight들은 연산(행렬곱)되어 좀전에 살펴본 sign 함수를 통해 output을 도출하게 됩니다.
이 output을 통해 -1이냐 1이냐에 따라 분류할 것입니다.
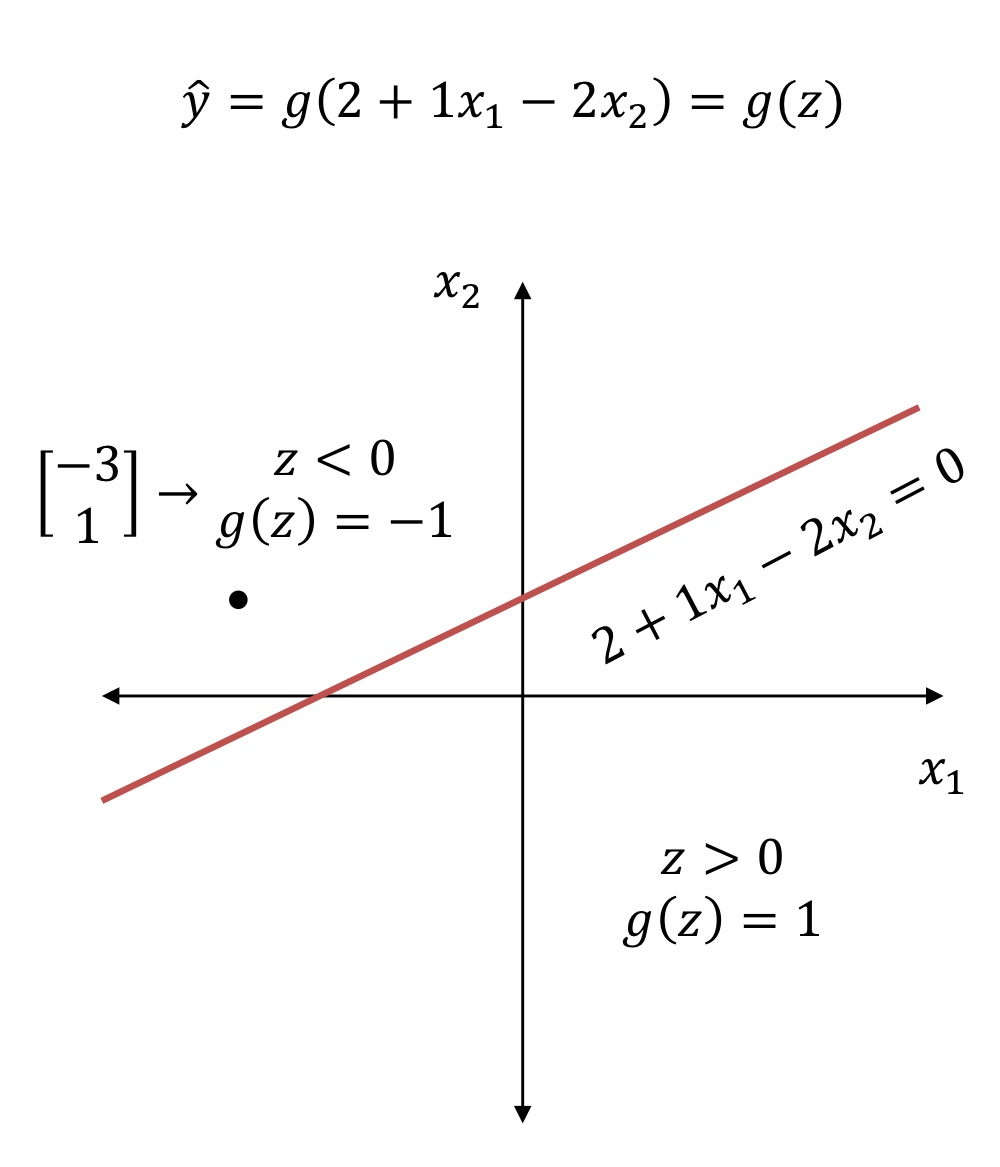
3. Learning XOR
- perceptron은 XOR 문제를 해결하지 못함
- perceptron의 linear한 hyperplane으로는 XOR 문제를 분류할 수가 없음
+ XOR
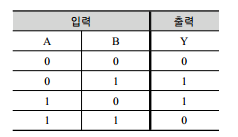
XOR은 무조건 A와 B가 다를 때만 1을 출력하게 됩니다.
공간을 통해 나타내면 아래와 같습니다.
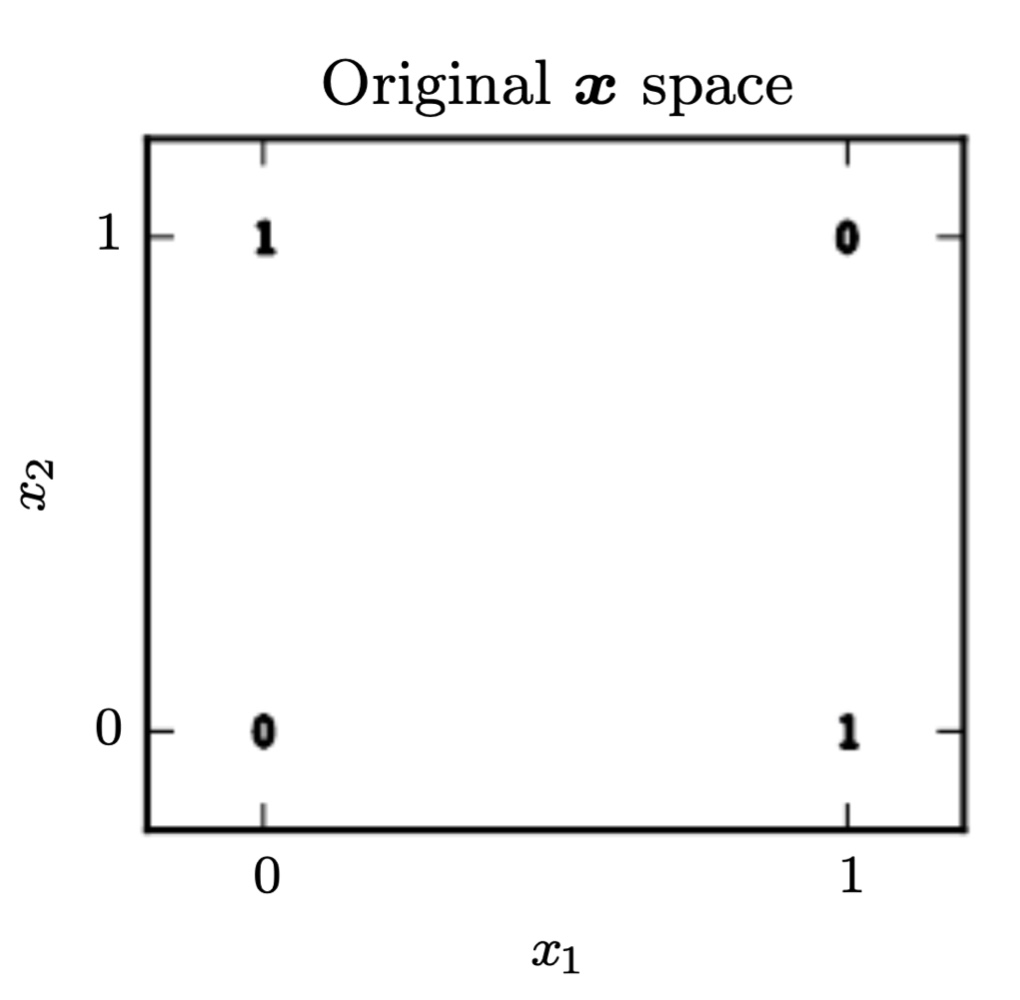
이러한 공간에서 linear한 선 단 하나로 0은 0끼리 1은 1끼리 분류할 수 있는 방법은 없습니다.
선 하나가 아니라 .. 아래와 같이 hyperplane을 두면 분류할 수 있지 않을까요?
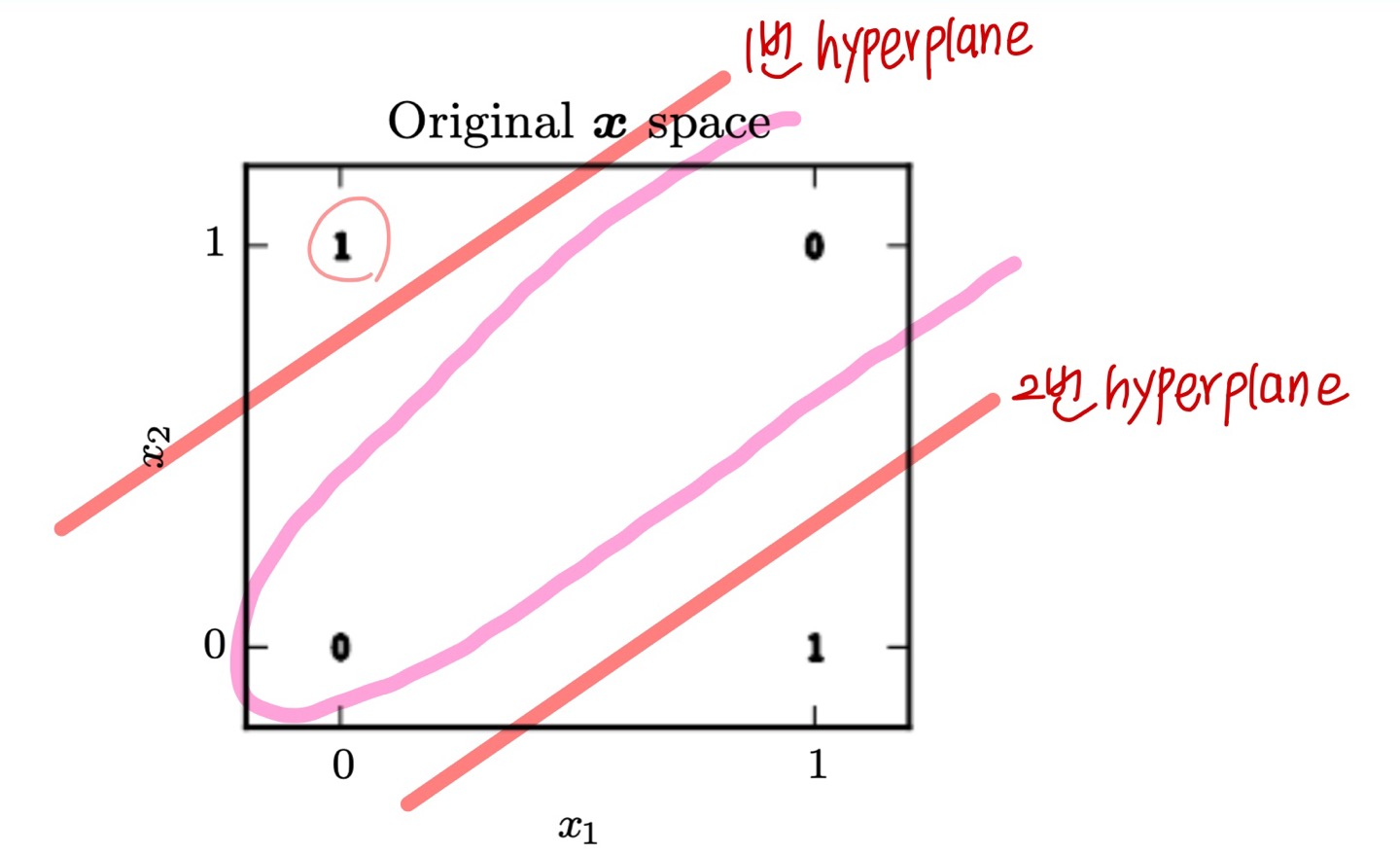
1번 hyperplane과 2번 hyperplane 즉 2개의 hyperplane을 두면 XOR 문제를 해결할 수 있지 않을까 하는 대안이 나오게 됩니다.
이 말은 1개의 perceptron과 또 다른 1개의 perceptron을 결합해서 분류하자는 말과 같은데요.
이것은 MLP의 시작이 되게 됩니다.
- Multi-Layer Perceptron(MLP)
- Multi-Layer Perceptron = Neural Network
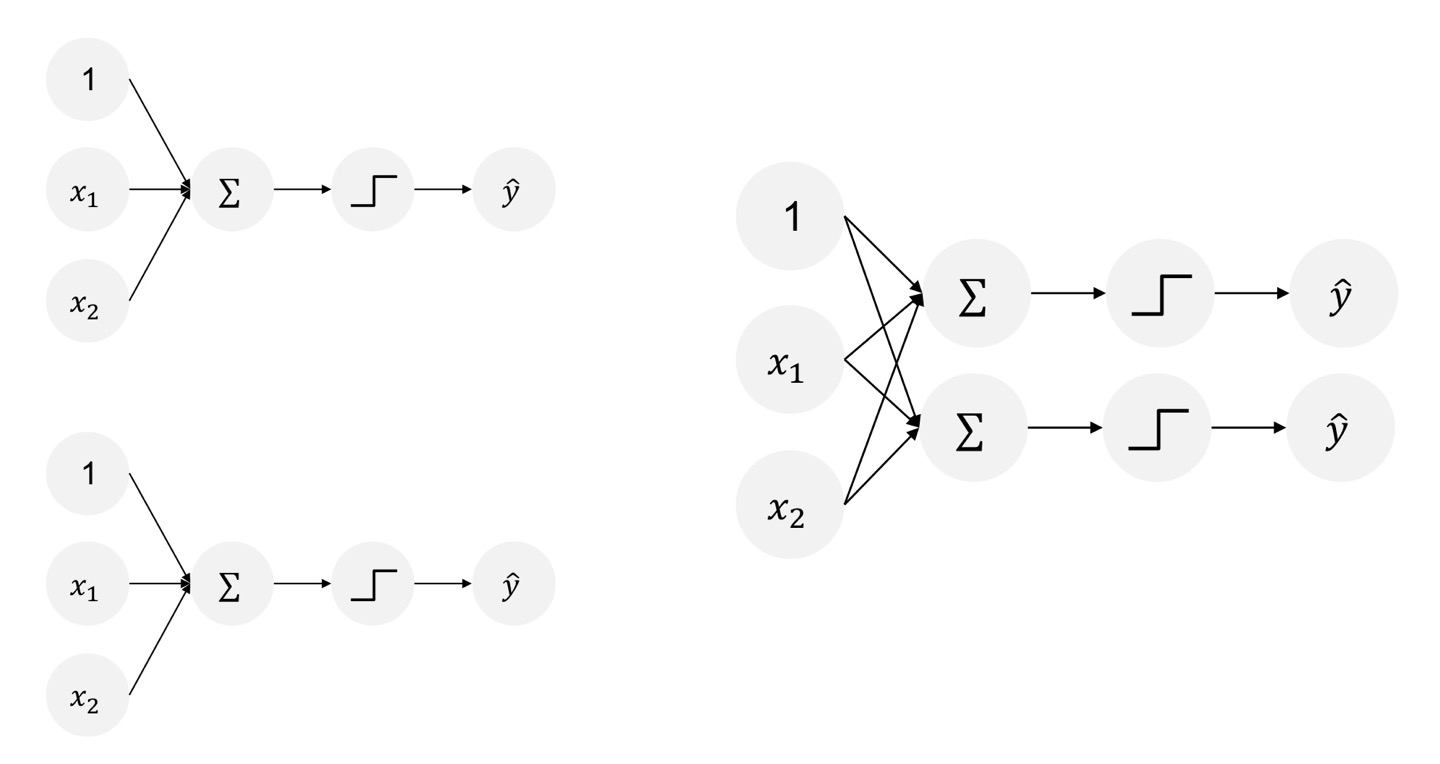
4. Multi-Layer Perceptron(MLP)
- MLP의 많은 layer와 많은 unit들로 구성되어 있는 perceptron이다.

- 비선형 분류(Nonlinear Classification)로서의 MLP - kernel mapping
위에서 XOR 문제는 비선형 hyerplane 2개를 이용하거나 비선형 함수를 이용하는 방법을 통해 분류를 할 수 있다고 했었습니다.
그렇지만 이제 소개할 방법은 linear한 hyperplane을 적용합니다.
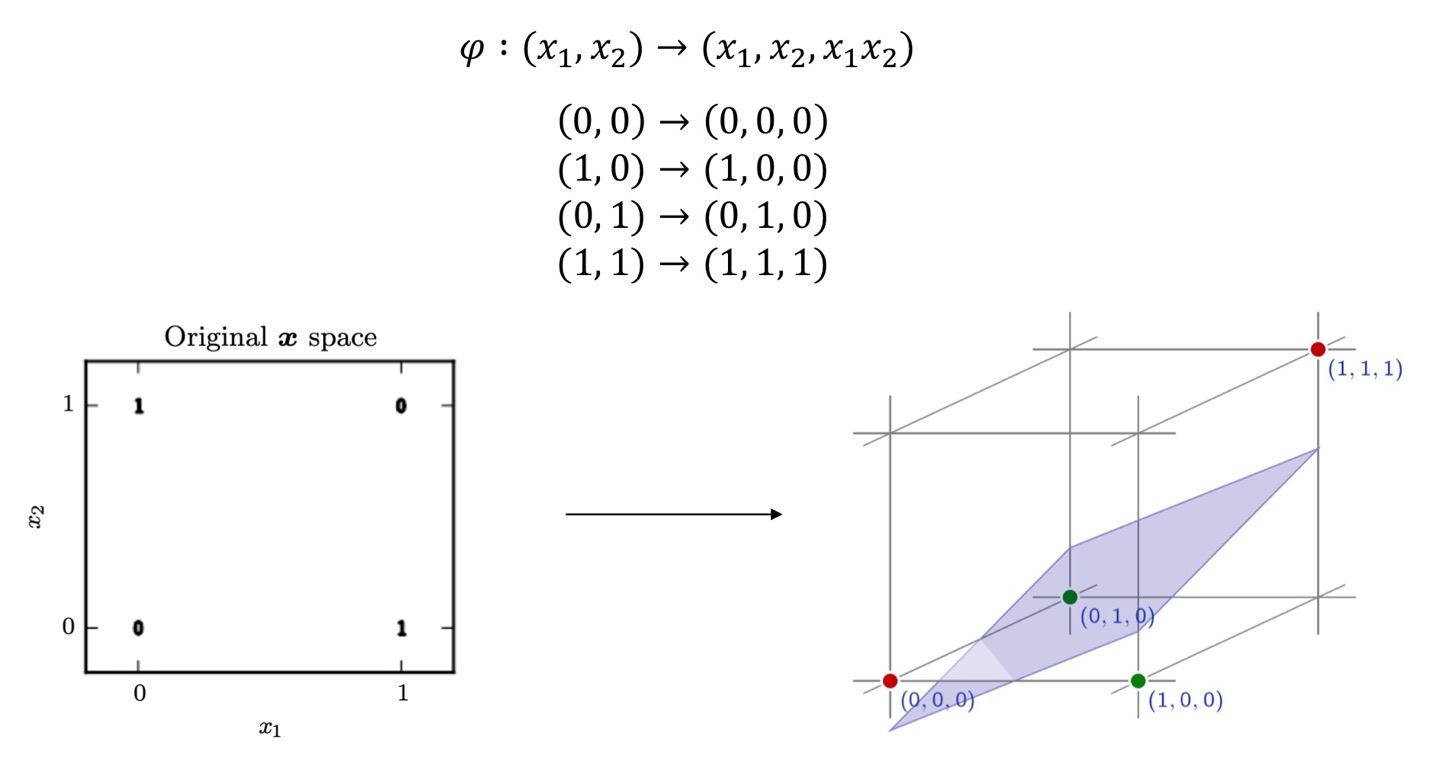
kernel이라는 mapping 함수를 사용하는 방법입니다.
- kernel mapping 함수로 새로운 변수를 추가하여 3차원으로 만들기
고차원으로 데이터를 변형을 하여 linear한 hyperplane을 적용하여 분류하는 방법입니다.
다시 돌아와서, MLP에서 분류(XOR 문제 포함)를 가능하게 하려면
MLP 내부에 kermel이 있으면 되겠죠?
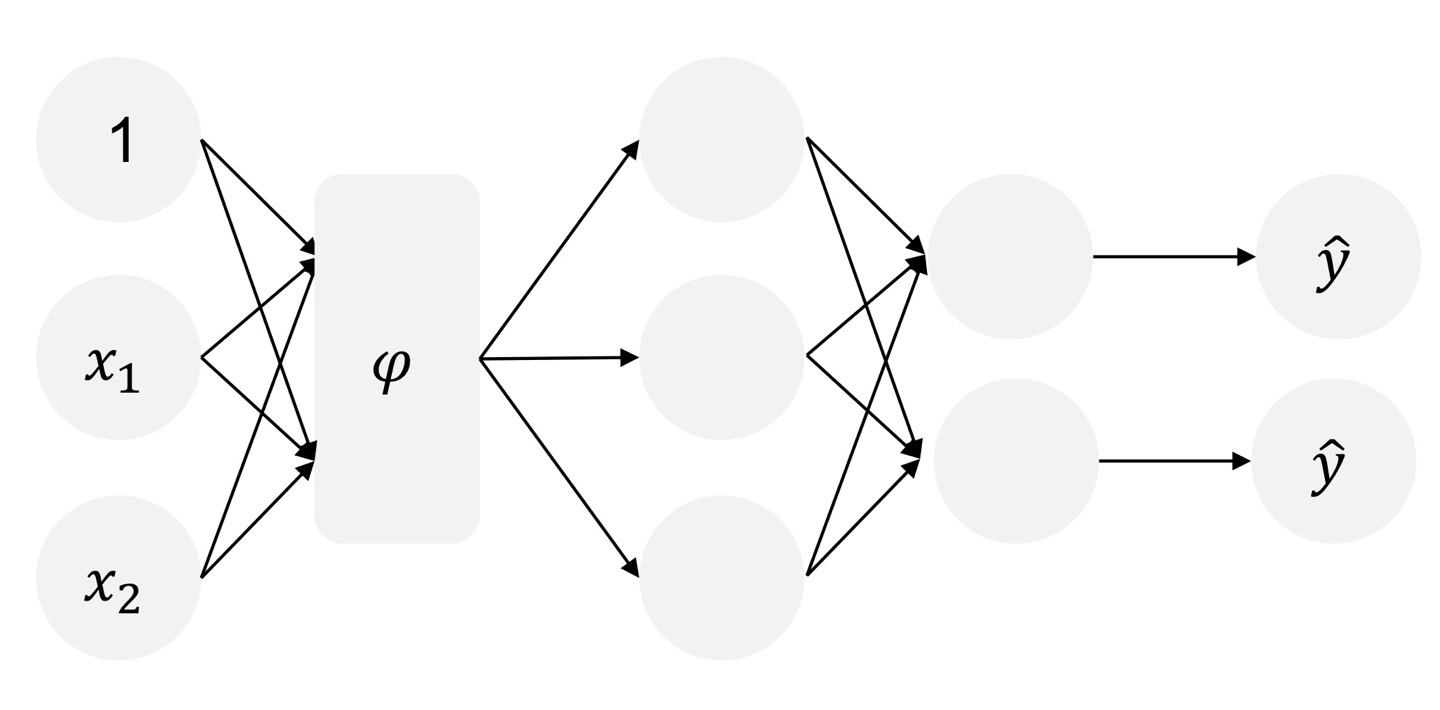
위 kernel 부분은 우리가 알고 있는 hidden layer 형태로도 보는 것이 가능합니다.
왜냐하면, 각각의 뉴런들이 모두 activation function을 포함하고 있기 때문입니다.
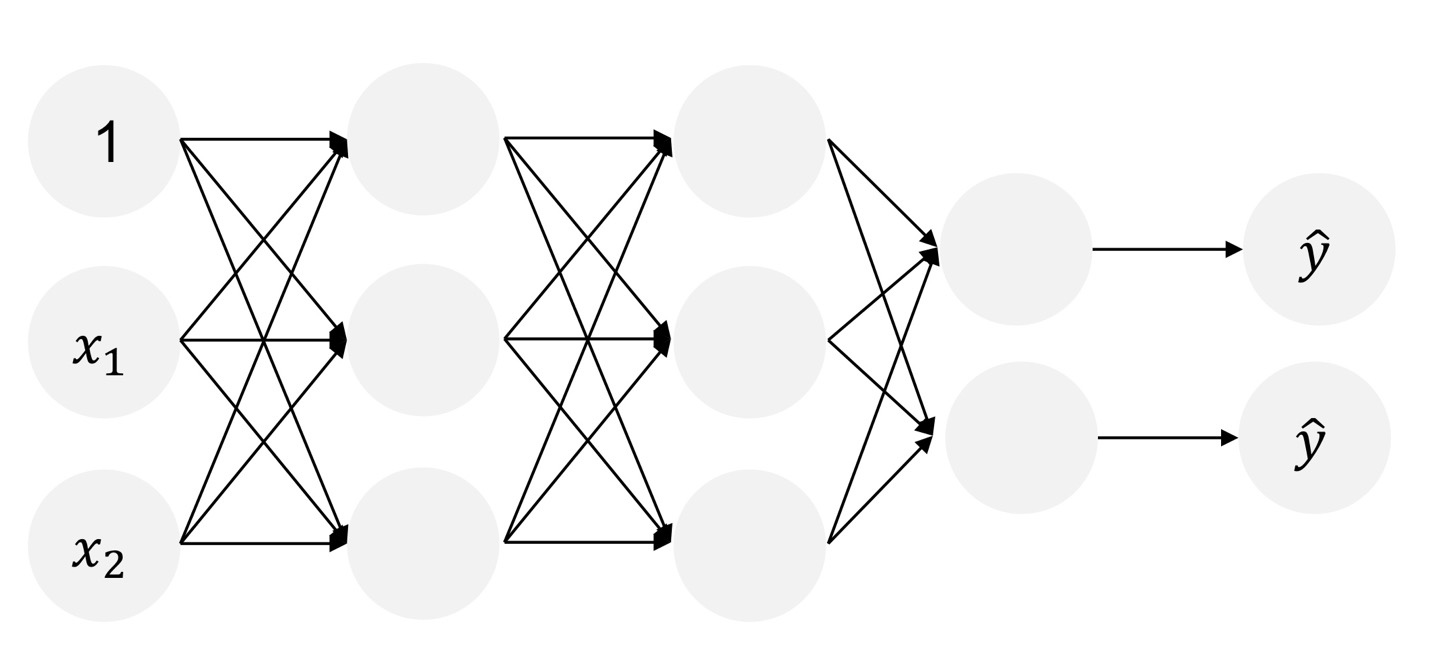
즉 다시 말해서, 우리는 kernel function으로 알고 있는 기능을 MLP에서는 hidden layer가 그 역할을 수행하여 Nonlinear 하게 바꿔서 classification을 가능하게 해준다는 것입니다.
5. Training MLP
- 학습 데이터를 통해 MLP의 weight(가중치)와 bias(편향)을 학습하기
- 학습을 잘 하려면?
- 최적화
- 손실 함수

- 예측값과 정답 사이의 오차를 최소화
① Non-linear optimization
- Gradient Descent
- Analytical solution이 아닌 iterative 방법을 활용
- Negative gradient 방향으로 이동시켜 gradient가 0에 가까워지는 지점을 찾음
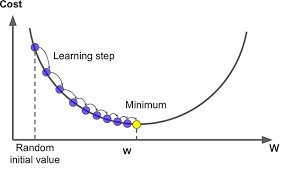
② MLP를 위한 Gradient Descent는 어떻게 작동?
- negative gradient 방향으로 이동시켜 오차가 줄어들도록 이동하여 최적의 weight를 찾음
- loss function의 미분값(기울기)가 감소하는 방향으로 점진적으로 이동
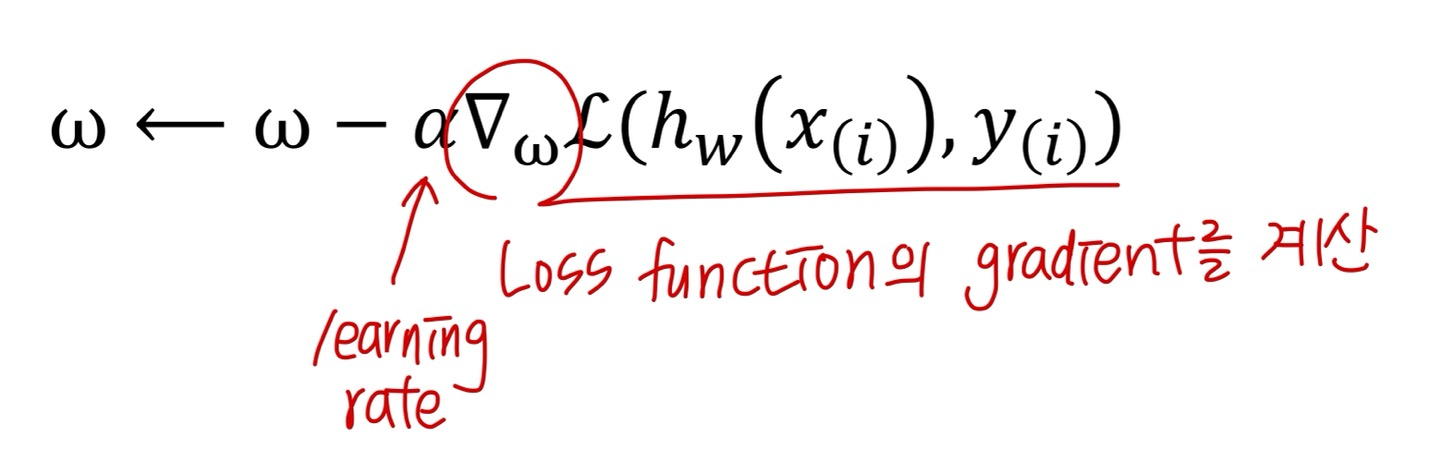
③ 최적의 weight는 어떻게 찾는가?
- 직접적인 방식으로 경사 하강법을 사용하여 데이터로부터 가중치와 편향을 학습
- 즉, 모든 점에 대해서 하나하나 계산
- 하지만, 굉장히 많은 연산이 필요해서 상당히 비효율적
- 이를 대체하기 위해 chain rule과 backpropagation 개념을 활용!
6. Chain rule and Backpropagation
① 연쇄법칙(Chain rule)
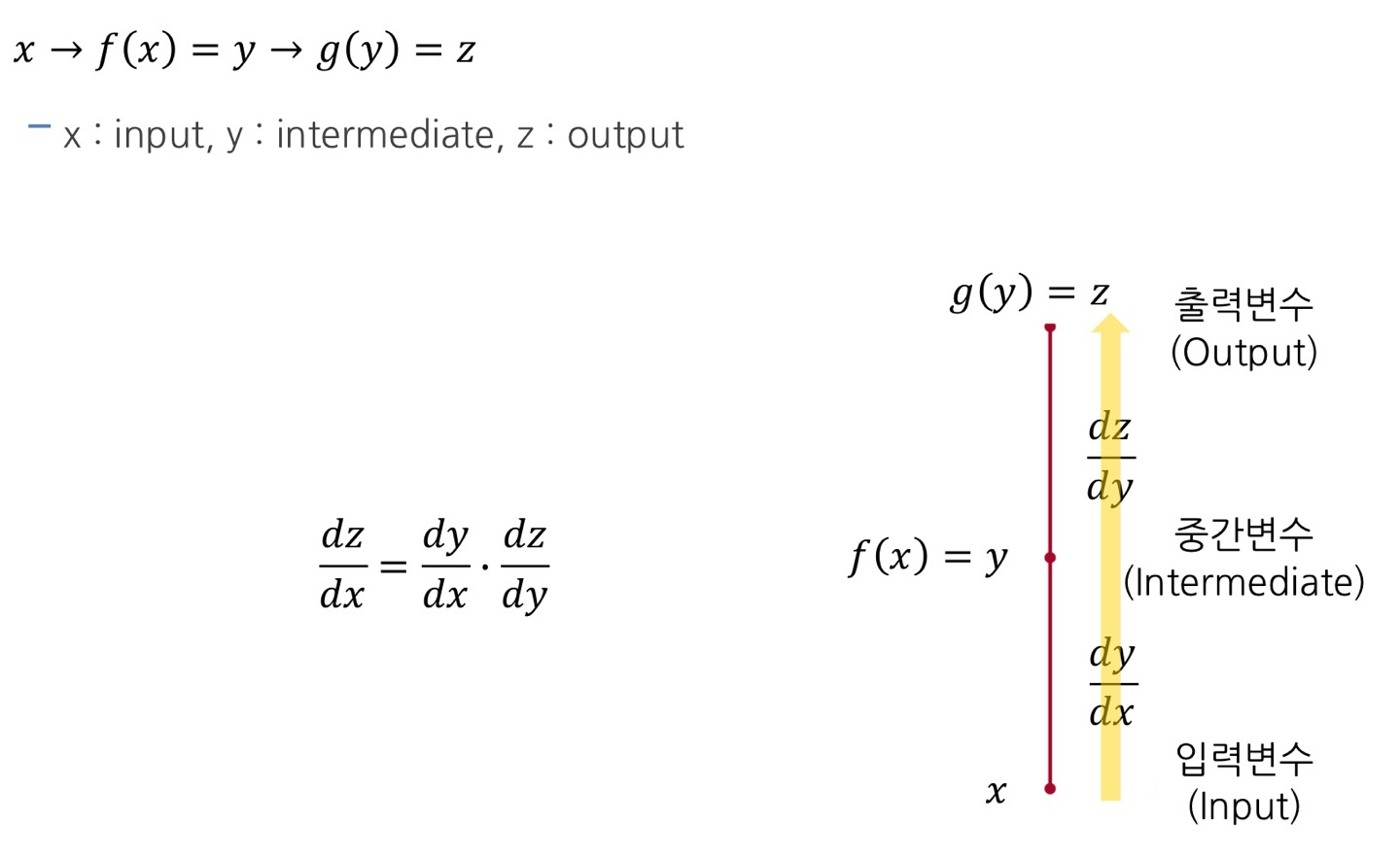
예시 1) 입력 1개, 중간 2개, 출력 1개
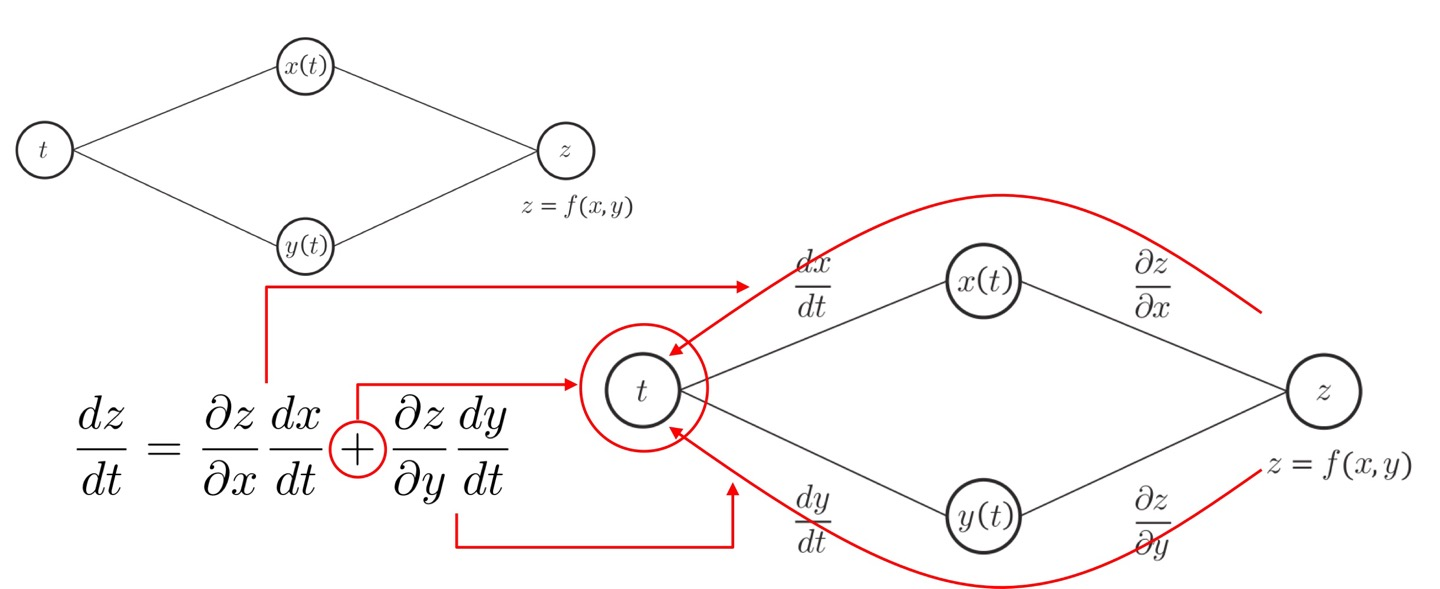
출력 변수의 입력 변수에 대한 미분값을 얻고 싶은데
중간 변수가 2개라면, 각각에 대해서 연산을 해서 sum으로 연결해주면 됩니다.
예시 2) 입력2개, 중간 2개, 출력 1개
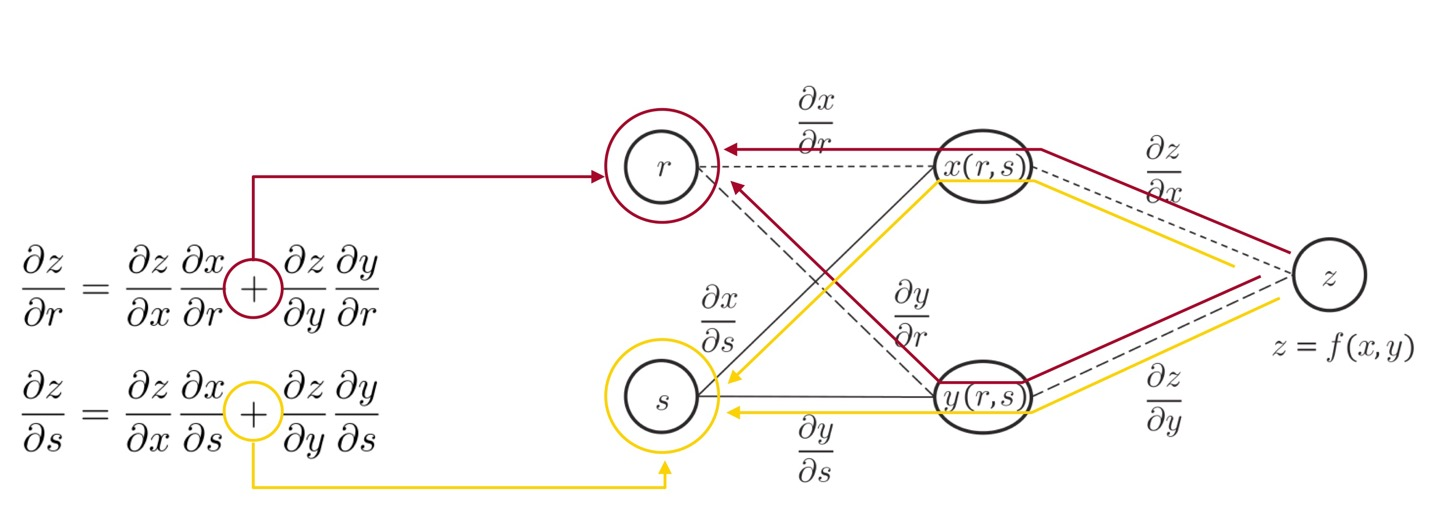
출력 변수의 입력 변수에 대한 미분값을 얻고 싶은데
입력 변수도 2개고 중간 변수도 2개라면,
우선 입력 변수에 대해서는 각각 미분값이 나와야 합니다.
또한 위에서 중간 변수가 2개 일 때는 각각 연산을 해서 더해주었듯이
각각 구한 중간 변수 2개를 sum 해주어 입력 변수 2개에 대해서 각각 계산을 해줍니다.
입력 변수가 여러 개이면 하나씩 결과 도출
중간 변수가 여러 개이면 각각 지나가는 경로(?)에 따라 계산해서 입력 변수따라 더해주기
문제)
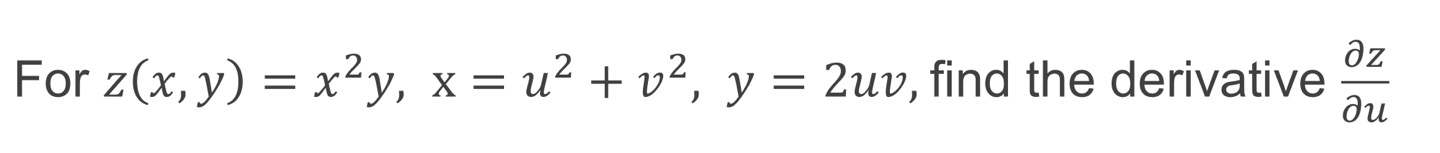
위 문제를 풀기전에 해당 문제의 neural network를 이해해보면... 아래와 같습니다.
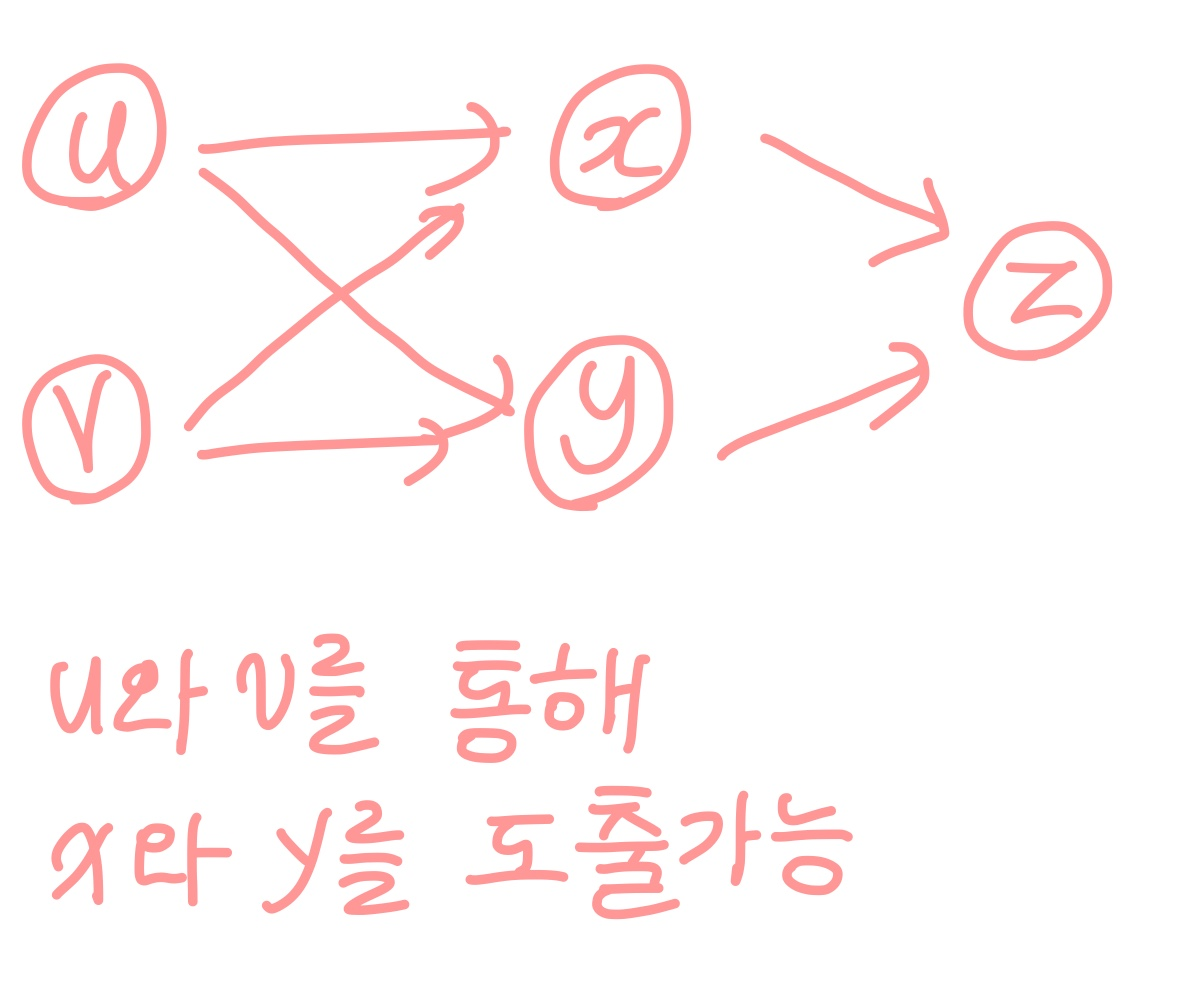
z(출력 변수)의 u(입력 변수 중 하나)에 대한 미분값이 궁금한 입니다. 일단은!
구조를 보면 입력 변수는 두 개(u와 v) 이고 중간 변수도 두 개(x와 y)로 그림으로 나타내면 위와 같습니다.
위에서 중간 변수가 2개라면 각각의 경로(?)에 대해서 연산을 해서 마지막에 더해주면 된다고 했습니다.
그러므로 (z의 x에 대한 미분값 * x의 u에 대한 미분값) + (z의 y에 대한 미분값 * y의 u에 대한 미분값) 이렇게 하면 되겠죠?
자세히 쓰면 아래와 같습니다.
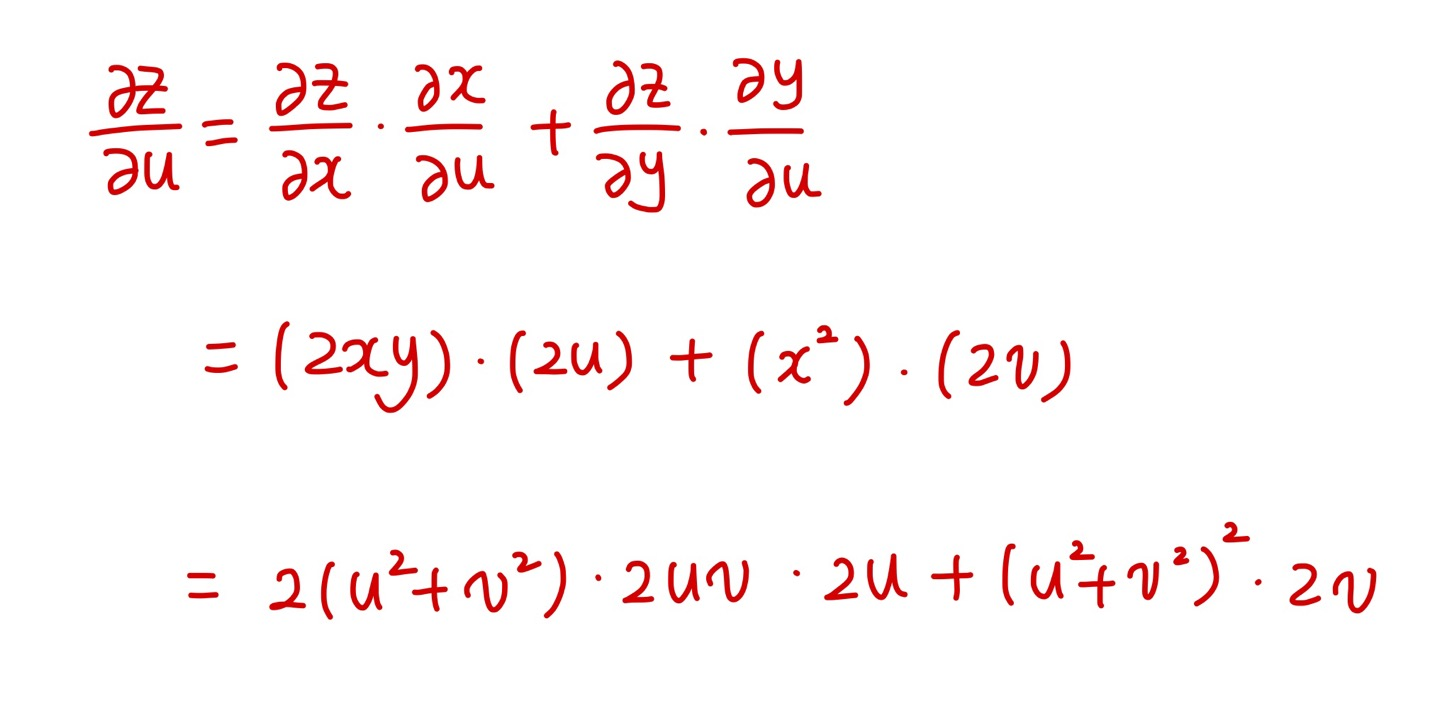
이 연쇄 법칙을 조금 일반화하여 neural network에 적용하면 다음과 같습니다.
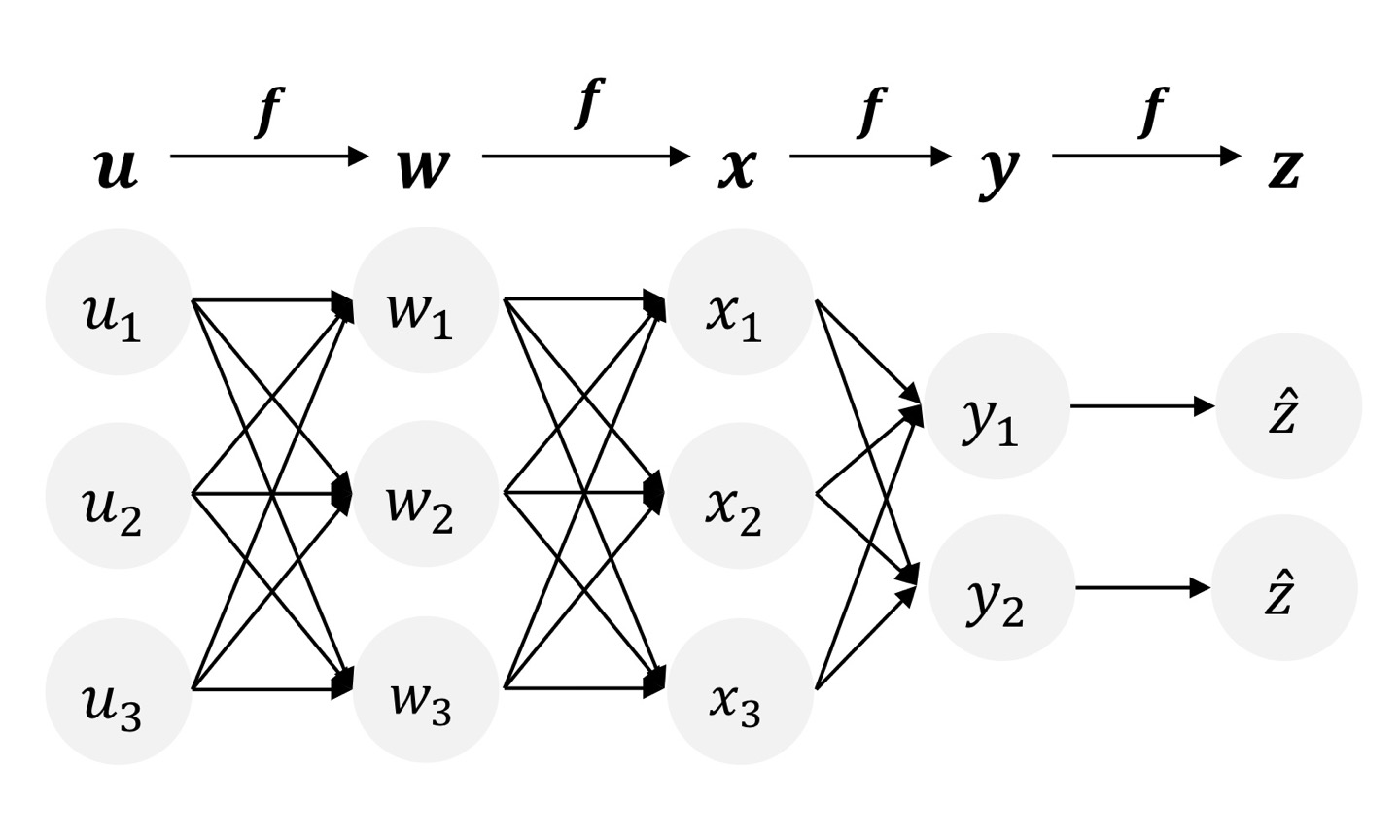
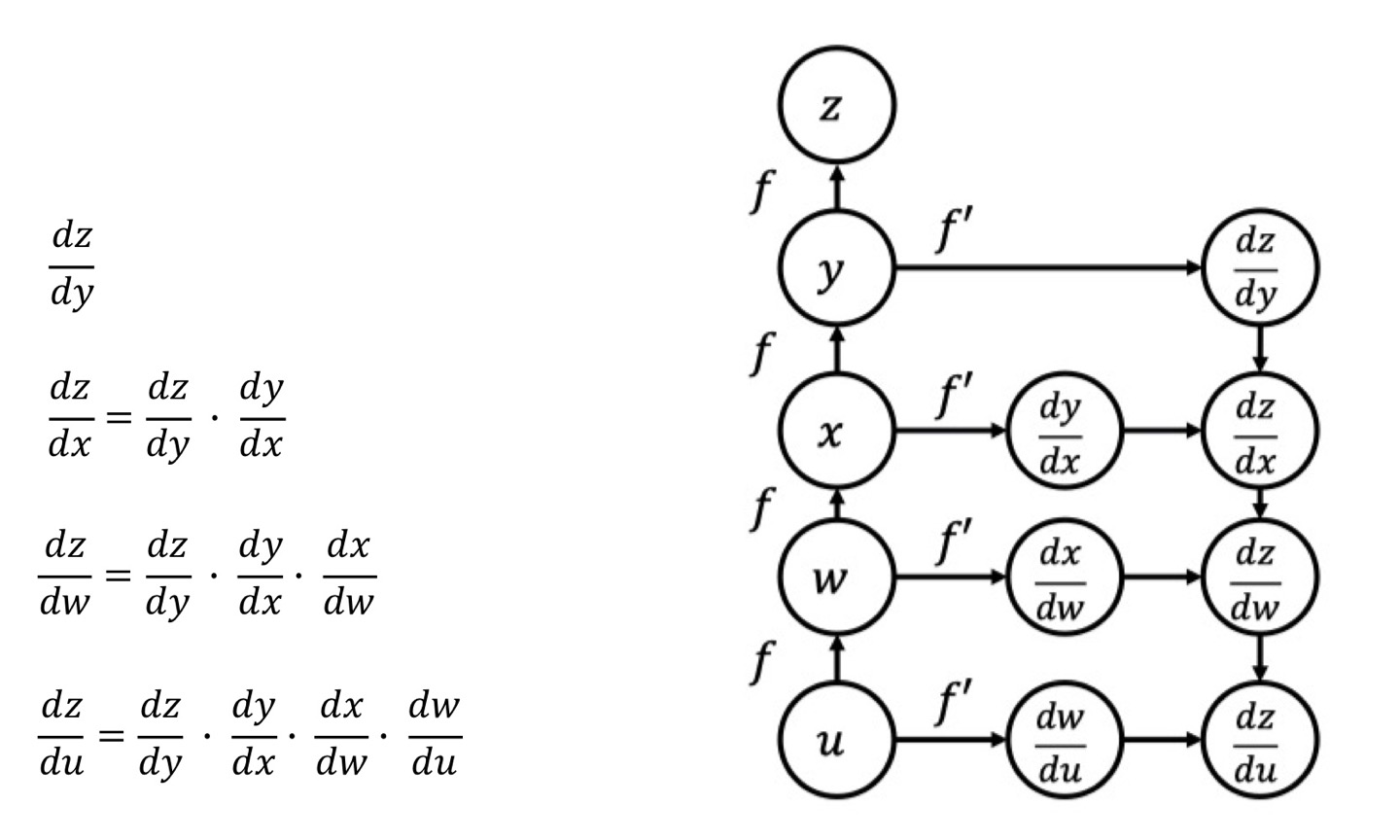
그런데 위 4개의 도함수들을 자세히 보면 바로 위 식에서 계산한 내용이 아래 식 내용에 포함되어 있고 하는 것을 확인할 수 있습니다.
바로 다음과 같이요!
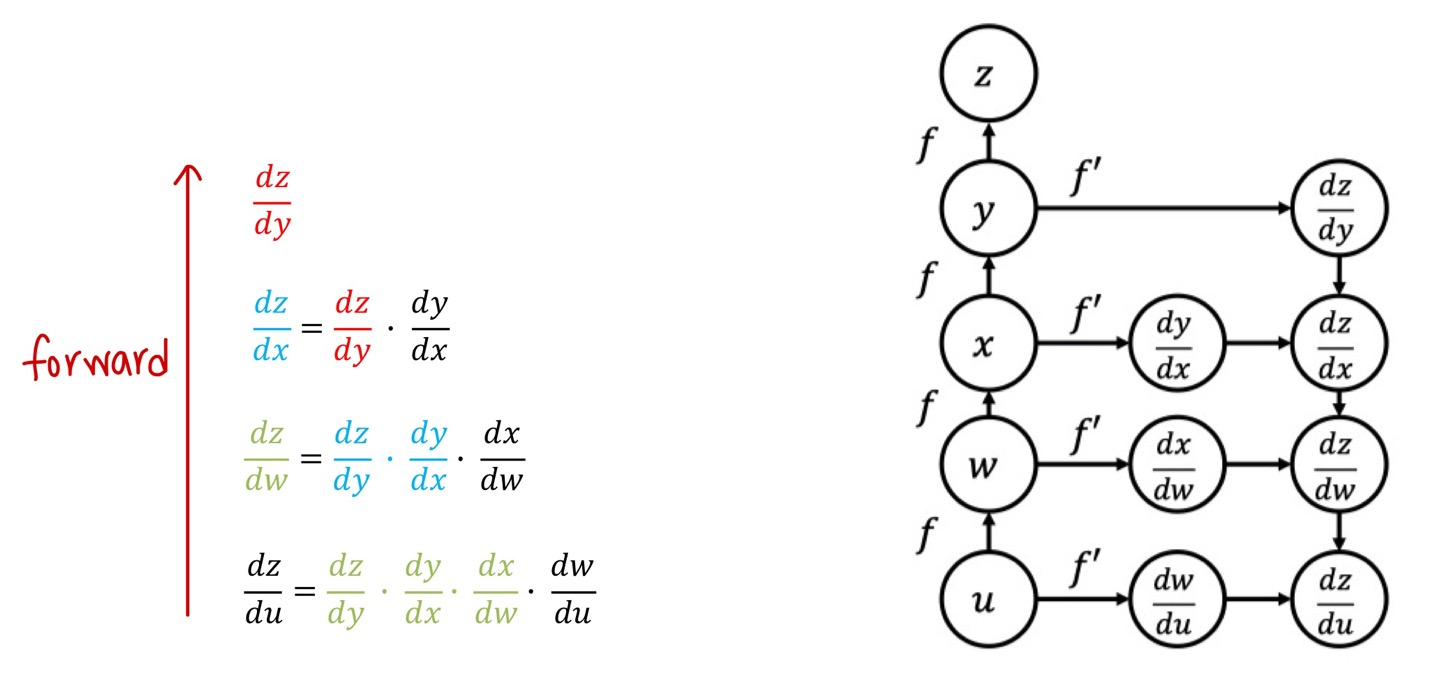
따라서 전부 다 연산을 하는 게 아니라 recursive하게 연산하면 일부만 새로 계산해도 최종적인 도함수까지 구할 수 있게 됩니다.
따라서 위의 그림에서 아래에서 위로 계산하는 forward 방식이 아니라 그 반대인 back 방향으로 연산을 하게 되면 recursive한 연산이 가능하다는 것입니다.
바로 이 방법이 backpropagation이 됩니다.
7. 최적의 weight를 구하기 위한 알고리즘 정리
① weight를 random하게 초기화
② chain rule로 gradient(weight)를 계산
③ weight를 업데이트
④ 2번과 3번을 수렴이 될 때까지 반복수행
⑤ weight들을 도출
'빅데이터 인공지능 > 딥러닝' 카테고리의 다른 글
| [딥러닝] 딥러닝에서의 일반화(Regularization) (0) | 2022.11.25 |
|---|---|
| [딥러닝] 딥러닝에서의 최적화(Optimization) (0) | 2022.11.25 |
| [딥러닝] CNN(Convolutional Neural Network)과 MLP(Multi Layer Perceptron) 의 차이 (0) | 2022.11.19 |
| [딥러닝] 딥러닝(ANN, DNN, CNN, RNN, SLP, MLP) 비교 (0) | 2022.11.19 |
| [딥러닝] CNN(Convolutional Neural Network) 모델 구현 (0) | 2022.09.18 |
- Total
- Today
- Yesterday
- 자바스크립트
- react-query
- next.js
- 프로젝트 회고
- react
- CSS
- 리액트 훅
- 리액트
- HTML
- 인프런
- 프론트엔드 공부
- 프론트엔드 기초
- 파이썬
- JSP
- 데이터분석
- jest
- TypeScript
- frontend
- 스타일 컴포넌트 styled-components
- Python
- rtl
- 타입스크립트
- 딥러닝
- styled-components
- 디프만
- 자바
- 자바스크립트 기초
- 프론트엔드
- 머신러닝
- testing
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
